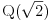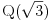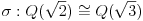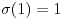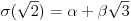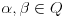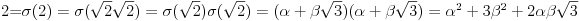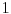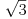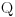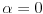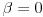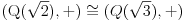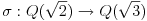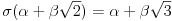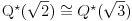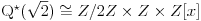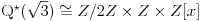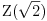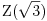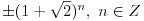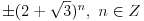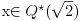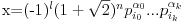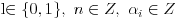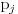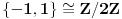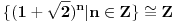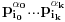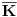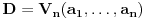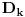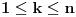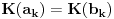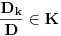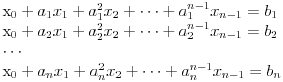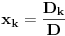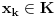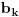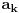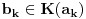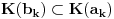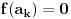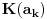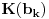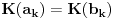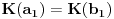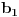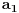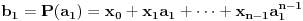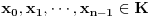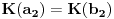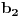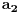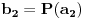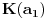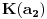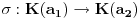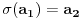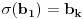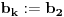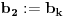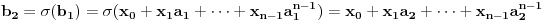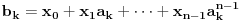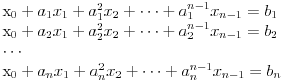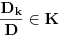Naci primere polja K i L koja nisu medjusobno izomorfna, ali su izomorfne njihove aditivne i multiplikativne grupe.
Znaci da bi trebalo da postoje dva razlicita izomorfizma
npr. f izmedju
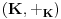 i
i 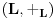
i g izmedju
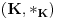 i
i 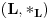
Bojane za slucaj da opet pozelis da mi obrises temu uz obrazlozenje:
>Moras da pokazes da si se potrudila i sama tako sto ces pokazati dokle si stigla i gde si tacno zapela.
Zapela sam na tome sto ne mogu da pronadjem ta dva polja. Pokusavala sam da ih nadjem danima ali zaista ne znam na koji nacin to da ti dokazem? Imam nekoliko svedoka koji su me videli kako se mucim, ne znam, hoces da ti posaljem kontakt telefone da proveris?
U pravu si, u pitanju jeste domaci, ali je eksplicitno naglaseno da smemo da koristimo svu mogucu literaturu i druge vrste pomoci, dozvoljena je saradnja i sl. Ako si toliko zaludan, mozes da proveris kod prof. Zarka Mijajlovica, Matematicki fakultet, Beograd.
Zasto ovo ne shvatis kao jos jedan zanimljiv zadatak na ovom forumu? Mozda ce se neko i zabaviti dok ga bude resavao, u svakom slucaju ne vidim kako moze da "steti kvalitetu foruma", "ne odgovara temi" ili krsi neko trece "pravilo"!
Usput, ne samo da ja nisam uspela da ga resim, nego ni cela treca godina teorijskog smera beogradskog Mat. fakulteta. Dovoljan izazov za ambiciozne? :-)
// sada sam postavila jos jedan neresen zadatak, ali sve navedeno vazi i za
//onaj koji si obrisao.




 malo teske algebre
malo teske algebre Re: malo teske algebre
Re: malo teske algebre