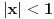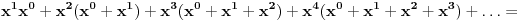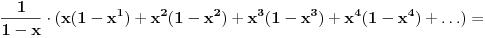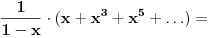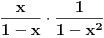xx0+x2(x0+x1)+x3(x0+x1+x2)+x4(x0+x1+x2+x3)+...
Hvala unapred svima koji se uključe u ovu temu.
[Ovu poruku je menjao Smilebey dana 12.02.2006. u 11:43 GMT+1]
"Na svetu postoje dve stvari koje su beskonačne. To su univerzum i čovekova glupost. Ali za univerzum nisam baš siguran!"
Albert Einstein
Albert Einstein




 Zadatak-geometrijski red
Zadatak-geometrijski red