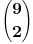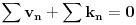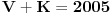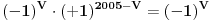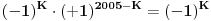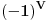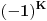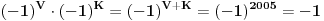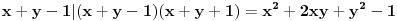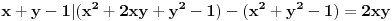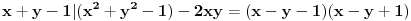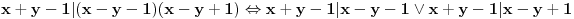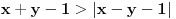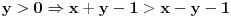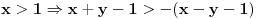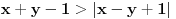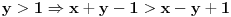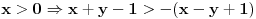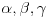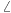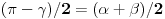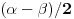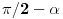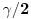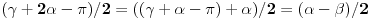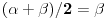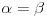1. Moguća su četiri slučaja:
a) Prva cifra je 1, dve od preostalih 9 su takođe 1, ostalo su 0. Takvih ima
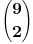
=36;
b) Prva cifra je 1, jedna od preostalih 9 je 2, ostalo su 0. Takvih ima 9;
c) Prva cifra je 2, jedna od preostalih 9 je 1, ostalo su 0. Takvih ima 9;
d) Prva cifra je 3, ostalo su 0. Takav postoji 1.
Ukupno 36+9+9+1=55.
3. Označimo proizvode po vrstama sa

, a proizvode po kolonama sa

. Pretpostavimo da je
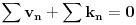
. Tada tačno 2005 od tih 4010 sabiraka mora biti jednako 1, a preostalih 2005 mora biti jednako -1. Označimo sa

broj negativnih

-brojeva, a sa

broj negativnih

-brojeva. Prema prethodno rečenom,
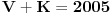
.
Ako izmnožimo sve

-brojeve, dobićemo proizvod svih brojeva u tabeli, a taj proizvod očito iznosi
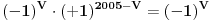
. Slično, ako izmnožimo sve

-brojeve, opet dobijamo proizvod svih brojeva u tabeli, a u tom slučaju taj proizvod iznosi
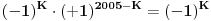
.
Međutim, brojevi
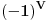
i
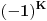
ne mogu biti jednaki, jer je njihov proizvod
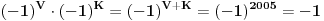
. Kontradikcija.
4. Pošto
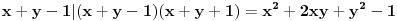
, sledi da
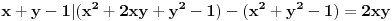
. Stoga
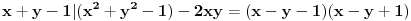
. Kada bi broj
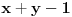
bio prost, moralo bi da važi
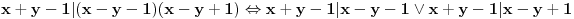
To je, međutim, nemoguće jer je
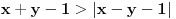
(pošto
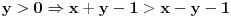
, a
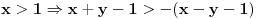
) i
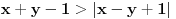
(pošto
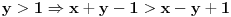
, a
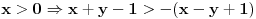
).
5. Neka je AM=BN=d, neka su uglovi trougla
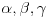
, neka je F središte stranice AB, neka je CK visina trougla ABC, neka simetrala ugla ACB seče pravu PQ u tački R i neka prava PQ, ukoliko nije paralelna pravoj AB, seče ovu u tački T (pri označavanju će se podrazumevati da je A između T i B). Tada je FQ srednja linija trougla ABM, pa je FQ=AM/2=d/2, a FP je srednja linija trougla ABN, pa je FP=BN/2=d/2. Dakle, trougao FPQ je jednakokrak. Pošto je
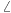
QFB=
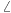
CAB=

i
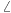
PFA=
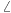
CBA=

, sledi da je
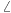
PFQ=

, pa je
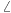
QPF=
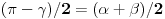
. Pošto je to istovremeno spoljašnji ugao trougla PTF, sledi da je
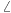
PTF=
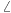
QPF-
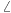
PFT=
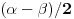
. S druge strane,
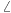
ACK=
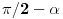
, a
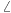
ACR=
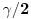
, pa je
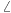
KCR=
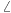
ACR-
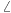
ACK=
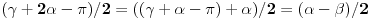
. Sledi da su uglovi PTF i KCR jednaki, pa pošto su im kraci CK i AB uzajamno normalni, takvi moraju biti i kraci CR i PQ.
Ako tačka T ne postoji, tj. ako je prava PQ paralelna pravoj AB, sledi da je
QPF=
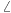
PFA, tj.
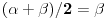
odn.
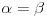
. Dakle, trougao ABC je jednakokrak s temenom u C, pa mu je visina na osnovicu istovremeno i simetrala temenog ugla, te je u tom slučaju simetrala ugla ACB normalna na pravu PQ jer je normalna i na pravu AB.
[Ovu poruku je menjao Farenhajt dana 25.12.2005. u 09:15 GMT+1]
 takav da se u zapisu broja
takav da se u zapisu broja 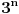 nalazi 2005 uzastopnih nula?
nalazi 2005 uzastopnih nula? i
i  prirodni brojevi veci od 1 takvi da je
prirodni brojevi veci od 1 takvi da je 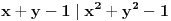
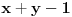 slozen broj.
slozen broj.



 Interno prvi razred
Interno prvi razred