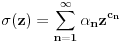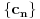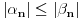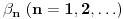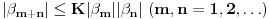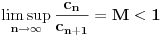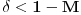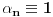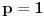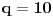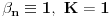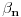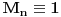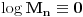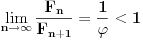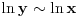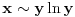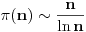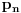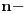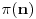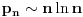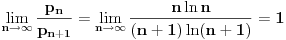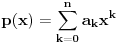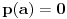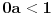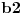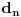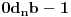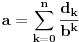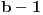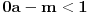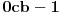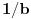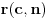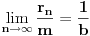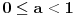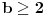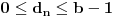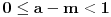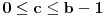BTW, LaTeX sa ovog foruma ne podržava komande \leqslant i \geqslant, nego se moraju koristiti \leq i \geq, pa u vezi s tim ispravljam greške koje su se potkrale u formulama.
Potvrdan odgovor na 3, a samim tim i na 1 sledi iz sledećeg iskaza:
Citat:
Svaki algebarski broj je racionalan ili normalan.
Ovaj iskaz nije dokazan. Predstavlja hipotezu koja je najverovatnije tačna. Pomenuti zadaci iz prve poruke za sada nisu rešeni (ne samo na ovom forumu, nego uopšte u matematici).
Navodim definicije:
A) Za kompleksan broj

kažemo da je algebarski ako postoji barem jedan polinom
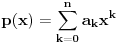
takav da su svi od brojeva

celi (odnosno racionalni) brojevi, od koji je barem jedan različit od nule i pri čemu je
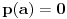
. U suprotnom se za kompleksan broj

kaže da je transcedentan.
B) Neka je

realan broj takav d aje
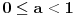
i neka je
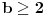
ceo broj. Tada postoji tačno jedan beskonačan niz celih brojeva
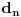
za koji važi
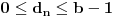
i
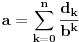
i pri čemu nisu svi elementi niza počev od nekog jednaki
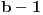
. Tada za niz
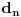
kažemo da je decimalni razvoj broja

u standardnom pozicionom sistemu sa osnovom

.
C) Za realan broj

se kaže da je normalan ako za svaki ceo broj
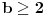
važi sledeće:
Neka je

jedinstveni ceo broj za koji važi
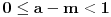
i neka je
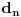
decimalni razvoj u standardnom pozicionom sistemu sa osnovom

. Tada za svaki ceo broj

takav da je
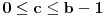
važi da mu relativna frekvencija pojavljivanja teži ka
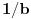
. Drugim rečima, ako je
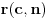
broj pojavljivanja broja

u nizu

(dakle, na prvih

mesta), onda je
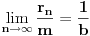
.
Ako iracionalan realan broj u svom decimalnom razvoju sadrži samo cifre 0 i 1, onda on nije normalan jer je frekvencija pojavljivanja cifre 2 jednaka nuli, pa prema navedenoj hipotezi ne može biti algebarski, odnosno transcedentan je.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
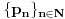 niz svih prostih brojeva. Da li je broj
niz svih prostih brojeva. Da li je broj 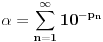 transcendentan?
transcendentan?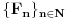 Fibonačijev niz s početnim vrednostima
Fibonačijev niz s početnim vrednostima 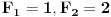 . Da li je broj
. Da li je broj 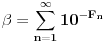 transcendentan?
transcendentan?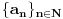 bilo kakav beskonačan monotono rastući niz prirodnih brojeva. Da li je broj
bilo kakav beskonačan monotono rastući niz prirodnih brojeva. Da li je broj 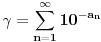 algebarski ako i samo ako je racionalan?
algebarski ako i samo ako je racionalan?



 Transcendentnost brojeva
Transcendentnost brojeva