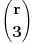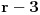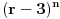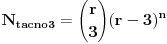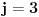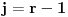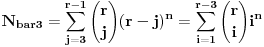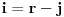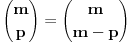Da li sam dobro uradio ili ne.Kombinatorika!!!Na koliko načina možemo n različitih predmeta razmjestiti u r različitih kutija, tako da tačno 3 kutije ostanu prazne? A barem tri prazne?
Riješenje:
Ja sam njuškajući po nekim knjigam, sveskam, skriptama...došao do zaključka da se ovo može predstavitikao broj svih surjekcija Nn->Nm.
=Σ(-1)^(x-j)(x nad j)*j^n (suma ide od 0 do x)
Gdje je x - broj kutija, a n - broj predmeta. U mom prvom slučaju x=r-3 i to je to.
Sada drugi dio zadatka koji kaže da barem tri kutije ostanu prazne. Znači mogu ostati 3,4,5,...,r-1 prazne kutije. Ja sam mislio da ovo napišem samo kao sumu svih ovih surjekcija. Tj. ako mi je (r-3) kutija popunjeno + (r-4) + (r-5) ... +(1). Znači predhodnu formulu da sumiram još od 1 do r-3.
Da li je ovaj moj način razmišljanja ispravan.Ako sam negdje pogriješio može li mi neko pomoći oko ovoga zadatka.
Centrometal CM 20-35kW
Re: Da li sam dobro uradio ili ne.Kombinatorika!!!
