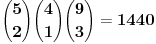Dobih i ja flešbek, pa me nije mrzelo da pogledam: „Analiza sa algebrom 2“ (Kadelburg, Mićić, Ognjanović), glava 5, zadatak 56.
Elem, rešenje jeste 540. Kao što Danilo reče, sve mogućnosti broja bekova, centara i krila su: (2, 1, 2), (3, 1, 1), (4, 1, 0), (2, 2, 1), (3, 2, 0) i (2, 3, 0). Tada je zbir svih kombinacija:
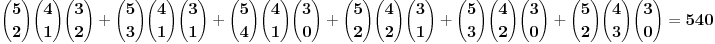
Rešenje 1440 bi bilo kad bi se zahtevalo da igraju
tačno dva beka i jedan centar. Tada bi, posle njihovog izbora, ostalo devet igrača koji mogu ravnopravno da se rasporede: