Citat:
Bojan Basic: Ne shvatam kako bi to išlo, lako je kad postaviš zadatak sa nekog takmičenja, ali šta ako neko postavi iz neke zbirke za pripreme i sl. gde ne piše koji zadatak je za koji razred?
paaa,ako je zbirka recimo za prvi razred....;)))))))))))))))
Citat:
Bojan Basic:
I. D. je imao 100 bodova, a P. M. je imao 99 sa obrazloženjem da su mu skinuli taj jedan bod zbog toga što je njegov kolega rešio zadatak korišćenjem matematičkog aparata koji je mnogo iznad njegovog nivoa, i na osnovu toga oni ne mogu biti jednaki na deobi prvog mesta!!! Naravno da ni ovo nije u redu, ali sve ovo pričam da bih ti objasnio da ti smeš da koristiš sve što matematika poznaje kao tačno, a kad je predsednik komisije izvesni profesor koji je i sad na vrlo visokoj funkciji (razumljivo je što mu ne pominjem ni inicijale) onda on može čak i da zaobiđe pravila da bi te nagradio za znanje.
hmhmhm...
ovdje je ja mislim situacija bila drugačija...(državno natjecanje)
naime,jedan je učenik(ne znam ime a ni inicijale :) ) mislim iz prvog razreda ili ne znam sad kojeg nije bitno,u jednom zadatku preskočio stranicu različitih matematičkih muljanja koja su dopuštena na njegovom nivou i jednostavno aparatom(znanjem)matematike viših razreda napisao neku tvrdnju iz koje lako dobiva rješenje.
e sad su nastale dileme u komisiji.jedan dio je mislio kako se riješenje treba 100% uvažit a drugi kako rješenje ne treba priznat kao potpuno(neki čak da ga treba prekrižit!!!!)nisam siguran ali mislim da je učenik "popušio" a sigurno nije dobio sve bodove
tada sam ja bio na strani učenika i smatrao sam da je to ispravno.
ali sada mislim drukčije,naime službena rješenja su UVJEK data na razini na kojoj je i zadatak,i u principu treba samo dobra ideja.
to je ono što ja mislim da je ispravno.govoreći konkretno o zadatku s početka teme, ja sam mogao "nabubat"te derivacije ili što već i neke jednostavnije primjere, i napisat rješenje a da uopće ne znam o čem je riječ,dok s druge strane ideja koja počiva na AG nejednakosti je jednostavna,dopuštena,elegantna,razumljiva itd... smatram da je to inteligencija,snalaženje u datim situacijama s DANIM sredstvima...
Citat:
Bojan Basic:
ove godine sam za jedno mesto omašio svetsku Olimpijadu
crnjak....
Citat:
Bojan Basic:
Dobro, mada malo preciziraj šta bi tačno voleo (npr. oblast), ne pada mi sad na pamet ni jedan zadatak koji bi ti se svideo ali u svakom slučaju ih mogu pronaći. I obavezno pregledaj ovaj forum, ima tu dosta lepih zadataka do sada objavljenih.
pa ne znam može bilo šta ali evo sad trenutno recimo neke nejednadžbe...
(evo konkretno malo AG nejednakosti)
možda imaš zadatke kad si ti bio prvi,pa ako moš njih poslat...(btw. kako se ti pripremaš za natjecanja?)
poželjan bi bio i pokoji link...ma svega...a i forum je dobra ideja
a što se tiče onog zadatka s pravokutnim trokutom mislim si ja nešt ovako:
Citat:
hellbound: 1.(pravougli trougao) ugao <CFD je prav zato jer je periferni ugao kružnice k nad njenim prečnikom CD. Takođe periferni ugao <ECF kružnice k, nad njenom tetivom EF je prav, pa je tetiva EF u stvari prečnik kružnice k. Lako je sada zaključiti da je CFDE u stvari pravougaonik, odavde pak sledi da je G centar kružnice k. Dalje, primetimo da je <CAB=<CFE. Neka je x tangens ugla <CFE tada x=CE/CF. Međutim imamo 4CG^2=CE^2+CF^2 i CG^2=CE*CF odavde izvodimo da mora važiti x^2-4x+1=0. Rešavanjem ove kvadratne jednačine dobijamo rešenja za x odakle lako dobijamo da su uglovi 15° i 75°.
sve je jasno do tangensa.i poslje toga je sve dobro ali mislim da je krajniji zaključak pogrešan,odnosno iz kvadratne jednadžbe dobivamo dva rješenja za tangens(slično kao i bojanovo rješenje gdje imamo dvje vrjednosti za p), a time i omjer(valjda) CE/CF pa bi valjda onda te dvije dužine trebale imati i dvje duljine što je ,opet valjda:))), nemoguće
iz uvjeta zadatka izlazi(a=CE,c=EF)
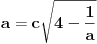
pa izlazi da je kateta u takvom trokutu uvjek veća od hipotenuze što je opet nemoguće...
budući da su svi postavljeni zadatci rješeni evo par novih :)) :
(na ovom sam natjecanju bio u sedmom razredu;))
-------------------------------------------------------------------
11. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Zadar, 2. - 5. svibnja 2002.
Zadatci za I. razred
1.Duljina srednjice trapeza je 4, a kutovi uz jednu osnovicu su 40 i 50 stupnjeva. Odredite duljine osnovica ako je udaljenost njihovih polovišta jednaka 1.
2.Dokažite da za bilo koje pozitivne brojeve a, b, c i bilo koji nenegativan cijeli broj p vrijedi nejednakost
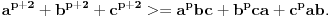
3.Nađite sve trojke (x,y,z) prirodnih brojeva koji zadovoljavaju jednadžbu
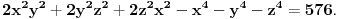
4."Kolo sreće" podijeljeno je na 30 odjeljaka u koje su upisani brojevi 50, 100, 150, ... , 1500 (u nekom redosljedu). Dokažite da postoje tri uzastopna odjeljka u kojima je zbroj brojeva veći ili jednak 2350.
-------------------------------------------------------------------
treći sam skoro riješio...a za prvi nisam siguran dal je rješenje točno,a četvrti je dost proziran dok drugi...u svakom slučaju,ko želi...
Blago onom tko rano poludi,
pa mu život u veselju prođe