Srodne teme

20.09.2005. Pomoc oko izbora dela za izvodjenje na Ele.Gitari
16.01.2006. Aksiome Neprekidnosti
23.03.2006. Zadaci iz geometrije za 1. gimnazije
31.03.2009. Njutnovi zakoni- dokaz
17.08.2006. literatura za I raz. M.gimnazije
24.08.2006. diferencijalna geomatrija
28.04.2007. kako ide izvodjenje za povrsinu lopte
11.09.2007. Zadatak iz geometrije
13.11.2007. Zbirka rešenih zadataka iz nartne geometrije
18.06.2008. Verovatno smaram, ali sta da radim

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Aksiome geometrije i izvodjenje

[es] :: Matematika :: Aksiome geometrije i izvodjenje

Strane: 1 2

[ Pregleda: 5897 | Odgovora: 21 ] > FB > Twit

Autor

Hiperbola

Član broj: 330522
Poruke: 6

Profil

Aksiome geometrije i izvodjenje

^{13.09.2015. u 20:54 - pre 117 meseci}

Upisao sam matematicki fakultet (Racunarstvo i informatika). I krenuo sam malo da cituckam geometriju iz knjige matematika za prvi razred gimnazije Jovan D. Keckic. Uvek su me bunili ti dokazi iz aksioma pa me brine da ja bas i nisam za ovaj fakultet.
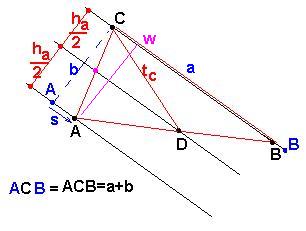
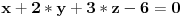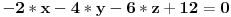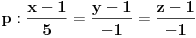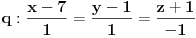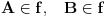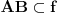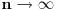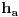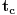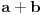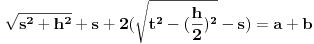Konkretan primer:
Aksiome veze
(A1) Svaka prava sadrzi najmanje 2 tacke.
(A2) Za svake dve razlicite tacke postoji jedna i samo jedna prava koja ih sadrzi.
(A3) Svaka ravan sadrzi najmanje tri nekolinearne tacke.
(A4) Za svake 3 nekolinearne tacke odredjuju jednu i samo jednu ravan.
(A5) Ako dve tacke neke prave pripadaju jednoj ravni, tada i ta prava pripada toj ravni.
(A6) Ako dve ravni imaju jednu zajednicku tacku tada one imaju najmanje jos jednu zajednicku pravu.
(A7) Postoje 4 nekomplanarne tacke.
To su aksiome kako stoje u knjizi.
Tvrdjenje kod kojeg je problem glasi ovako.
Ako dve razlicite ravni imaju jednu zajednicku tacku, tada te ravni imaju jednu i samo jednu zajednicku pravu.
Ja bih to ovako dokazao.
Zajednicka tackau obelezimo sa

a ravni sa

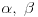
Po aksiomi (A6) te dve ravni imaju jos jednu zajednicku tacku

. Kako sada imamo dve razlicite tacke po (A2) imamo jednu pravu

.
Vazi po tvrdjenu zadatka

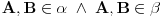. Sada po aksiomi (A5) imamo da

.
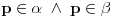I tu bi ja stao i smatrao da je zadatak zavrsen(tvrdjenje dokazano).
Dokaz po knjizi:
Neka je A zajednicka tacka ravni

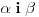. Na osnovu (A6) postoji jos jedna zajednicka tacka

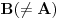tih ravni. Na osnovu (A2) postoji tacno jedna prava

kojoj pripadaju tacke

i

. Kako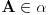

,

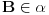na osnovu (A5) zakljucujemo da

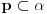i slicno

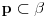. Tacke prave p jedine su zajednicke tacke ravni alfa i beta, jer kada bi postojala tacka S van prave p koja pripada i ravni alfa i ravni beta, tada bi na osnovu tvrdjenja (T) bilo

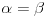, suprotno pretpostavci.
Tvrdjenje (T) Ako tacka A ne pripada pravoj p, postoji jedna i smao jedna ravan koja sadrzi tacku A i pravu p.

Ono sto je meni ovde problem je sto se nikad ne bi dosetio da se pozovem ovde na drugo tvrdjenje i dokazem kontradikcijom. Uopste to ne bih registrovao kao mogucnost. Kad procitam ceo dokaz meni deluje ok i da tako treba, ali ja uvek zaboravim nesta.
Moje pitanje je kako znati da je posao dovrsen do kraja?
Kad prelistavam i citam npr geometriju meni to deluje opako tesko(u smislu kolicine aksiome + teoreme + definicje). Kako se geometrija radi na fakultetu? Ne bih voleo da se pretvori u bubanje 1000+ neidentifikovanih letecih pojmova. A onda sporo shvatanje dokaza iz analize,algebre.... Da li je to sve uslovljeno nedostatkom vezbe i predavanja koja su usmerena na taj vid rada ili je to problem nedostatka sive mase :D .(Mi smo u gimnaziji samo cepali zadatke)

Odgovor na temu

djoka_l
Beograd

Član broj: 56075
Poruke: 3570

Jabber: djoka_l

+1527 Profil

Re: Aksiome geometrije i izvodjenje

^{13.09.2015. u 21:23 - pre 117 meseci}

Ti u tvom dokazu nisi dokazao da je prava jedinstvena samo da postoji.

Sledeća teorema važi:
Leme:
Postoji student na matematici, koji zna da dokaže geometrijsku teoremu.
Teorema se može dokazati samostalno, ili da se nauči napamet.
Svaki student koji završi matematički mora da položi geometriju.

Teorema:
student može da završi matematički ako zna da dokaže teoreme ili ih nauči napamet.

Odgovor na temu

Hiperbola

Član broj: 330522
Poruke: 6

Profil

Re: Aksiome geometrije i izvodjenje

^{13.09.2015. u 21:41 - pre 117 meseci}

Da li to moram da doakzujem kad po (A2) svake dve razlicite tacke odredjuju tacno jednu pravu. Zar to nije dovoljno?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.ptt.rs.

+2801 Profil

Re: Aksiome geometrije i izvodjenje

^{14.09.2015. u 16:58 - pre 117 meseci}

A šta ako ta druga zajednička prava ne prolazi kroz neku od tačaka A, B?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Hiperbola

Član broj: 330522
Poruke: 6

Profil

Re: Aksiome geometrije i izvodjenje

^{14.09.2015. u 17:56 - pre 117 meseci}

Onda se ravni poklapaju.

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
*.vs.rs.

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{15.09.2015. u 23:27 - pre 117 meseci}

Prepravi aksiomu (A6).
Pogrešno je napisana.

Pokazao si postojanje te prave, ali ne i jedinstvenost.

Ako su ti se više sviđaju zadaci:

Ravan alfa:

i ravan beta:

sadrže taćke P(1,1,1) i Q(6,0,0), pa time

i njihovu pravu

.

Ali sadrže i tačku R(7, 1, -1) pa time sadrže i

pravu

, koja je različita od prave p.

_{[Ovu poruku je menjao miki069 dana 16.09.2015. u 01:44 GMT+1]}

Odgovor na temu

Hiperbola

Član broj: 330522
Poruke: 6

Profil

Re: Aksiome geometrije i izvodjenje

^{16.09.2015. u 08:58 - pre 117 meseci}

Nazalost ja ne znam analiticku geomtriju u prostoru. Ovu u ravni razbijam. Meni zadaci nisu problem za njih sam izdresiran da ih tamanim, ali eto za ove druge "zadatke" i nisam bas toliko dobar.
Evo na primer: dokazati da je kruzna povrs konveksna figura.
Onaj gore zadatak bi mozda i mogo da se dosetim za jedinstvenost ali sta sa ovim? Ni ujednoj srednjoskolskoj knjizi nema dokaz za konveksnost bilo koje povrsi, ali to nije sprecilo autore istih da daju zadatak. Kako ja sad da znam sta je tu dovoljan dokaz i odakle u opste treba krenuti kad nisam video ni jedan jedini primer.
Figura je konveksna ako za dve tacke

vazi

I definicija kruzne povrsi: skup tacaka svih poluprecnika.
Nemam blage veze da to povezem.

Moja greska u pisanju.
(A6) Ako dve razlicite ravni imaju jednu zajednicu tacku, tada one imaju najmanje jos jednu zajednicku tacku.

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
*.vs.rs.

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{16.09.2015. u 16:11 - pre 117 meseci}

Nisam ni očekivao da znaš jednačine ravni i prave u prostoru, jer se to ne radi u srednjoj školi.
Očekivao sam da zaključiš da su ravni alfa i beta jedna te ista ravan, te da imaju istu jednačinu.
Ako jednačinu ravni alfa pomnožiš sa -2 dobija se ravan beta.

I ja mrzim geometriju.
Za samu kružnicu (gornju ili donju) bi se lako, preko drugog izvoda dokazala (konkavnost ili konveksnost).

Za ceo krug kao figuru?
Malo mi je i čudna ta definicija kruga. Možda ima neka bolja.
Probaj preko upisanog n-tougla, pa onda n teži u beskonačnost.
Čisto da bude rešenje iz analize, a ne iz geometrije.

Odgovor na temu

Hiperbola

Član broj: 330522
Poruke: 6

Profil

Re: Aksiome geometrije i izvodjenje

^{16.09.2015. u 18:41 - pre 117 meseci}

Mozda da definisem pojmove preciznije. Krug(kruzna linija) skup tacaka u ravni na jednakoj udaljenosti od neke date tacke. A kruzna povrs je ono sto sam naveo u prethodnom postu.
To sa n-touglom nije losa ideja. Svaki pravilni n-tougao upisan u krug mozemo da posmatramo kao presek n poluravni. Kako su poluravni konveksne tada je i figura koja se nalazi u njihovom preseku konveksna. Normalno

i tako dobijamo krug. Nazalost to nije cist geometrijski pristpu koji se trazi i koji ce mi trebati za predmet geometrija.
Sumnjam da se takav rezon trazi od ucenika prvog razreda srednje (za koje je pisan udzbenik) a jos manje ideja sa granicnim vrednostima + ne znam da dokazem da je polaravan konveksna.

Ja obozavam matematicku analizu. Geometriju volim ali ne toliko, ostale oblasti tu i tamo.

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
*.vs.rs.

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{16.09.2015. u 21:08 - pre 117 meseci}

Ako je O centar kruga i

Tvrđenje se svodi na dokaz da je OB ili OA maksimalna dužina duži OT, gde T tačka duži AB.
Što mislim da i nije teško da se dokaže. Bar nije teško preko sinusne teoreme.

Evo ti link do slične knjige za I razred matematičke gimnazije: https://imi.pmf.kg.ac.rs/moodle/mod/resource/view.php?id=2925

Odgovor na temu

Hiperbola

Član broj: 330522
Poruke: 6

Profil

Re: Aksiome geometrije i izvodjenje

^{17.09.2015. u 20:58 - pre 117 meseci}

Hvala za knjigu i ideje.

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
*.vs.rs.

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{17.09.2015. u 23:30 - pre 117 meseci}

Može preko Pitagorine teoreme.
Neka je O centar kruga i

.
Neka je OB>OA (sličan je dokaz i ako je OB<OA ili OB=OA).

Neka je T proizvoljna tačka duži AB.
Povucimo visinu iz temena O na pravu AB i neka visina seče pravu AB u tački F.
Pravougli troglovi OFT i OFB imaju istu katetu OF, a kateta FT je manja ili jednaka od katete FB,
tako da je po Pitagorinoj teoremi je hipotenuza OT manja ili jednaka od hipotenuze OB.
Time je dokazana konveksnost kruga.

Nedostaje dokaz Pitagorine teoreme, a to nije teško, ako je potrebno.

Odgovor na temu

berazorica

Član broj: 246954
Poruke: 165
*.dynamic.isp.telekom.rs.

+127 Profil

Re: Aksiome geometrije i izvodjenje

^{20.09.2015. u 08:40 - pre 117 meseci}

Ako je tema Aksiome geometrije i izvođenje, onda je glupo uplitati analitičku geometriju, pa i Pitagorinu teoremu, koja je teorema EUKLIDSKE geometrije, a ne apsolutne.

Znači, ovo je samo prva grupa aksioma, a prve četiri grupe čine apsolutnu geometriju (aksiome pripadanja, poretka, podudarnosti i neprekidnosti). Proširenje apsolutne geometrije aksiomom paralelnosti daje euklidsku ili neeuklidsku (npr. hiperboličnu) geometriju.

Za dokaze teorema koristiš samo ovaj spisak aksioma i to je dovoljno. Možda nekom nije simpatična ova geometrija u kojoj se dokazuju "očigledne" stvari, ali se tako najslikovitije ulazi u matematiku kao nauku - učiš kako se čitave teorije grade polazeći od jednog sistema aksioma (polaznih tvrđenja koja čine neprotivrečan, nezavisan i potpun sistem), pa preko jednostavnih tvrđenja, koja se izvode iz aksioma, dolaziš do mogućnosti da dokažeš najkomplikovanije teoreme.

Nemoj da se plašiš da će ti biti teška geometrija na fakultetu. U početku treba da se navikneš na ove početne teoreme, ali kad ih jednom dokažete, onda ćete ih nadalje koristiti, nećete se stalno vraćati na početna tvrđenja i aksiome.

"We are mathematicians, we are happy when we have a problem!"

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.200.247.*

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{20.09.2015. u 13:41 - pre 117 meseci}

Onda preko slicnosti.

_{[Ovu poruku je menjao miki069 dana 20.09.2015. u 14:59 GMT+1]}

Odgovor na temu

hotchimney

Član broj: 300237
Poruke: 462

+822 Profil

Re: Aksiome geometrije i izvodjenje

^{24.09.2015. u 08:54 - pre 116 meseci}

Citat:

Evo ti link do slične knjige za I razred matematičke gimnazije:
https://imi.pmf.kg.ac.rs/moodle/mod/resource/view.php?id=2925

Šta znači komplanarno?
Lučić u svojoj knjizi koristi koplanarano.
Ako je komplanarno onda je i komlinearno.
Medjutim svi kažu kolinearno.
Ko je nepismen?

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
*.vs.rs.

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{12.10.2015. u 08:56 - pre 116 meseci}

Konstruisati trougao ABC ako je dato:

je visina iz temena A

je težišna duž iz temena C

zbir stranica a i b.

Sve ideje sam ispucao i ništa nisam uradio.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.customer.blic.net.

+197 Profil

Re: Aksiome geometrije i izvodjenje

^{13.10.2015. u 01:28 - pre 116 meseci}

Ako imaš tri nezavisna karaktera trokuta koji definišu sve ostale njegove veličine,to ne znači da se rješenje mora naći pomoću šestara i lenjira.

U ovom tvom slučaju to se može rješiti analitički.Dakle imaš zbir dvije stranice (a+b),jednu visinu (h(a)) i dužinu težišnice (t(c)).
Analitika:
1)Povuci dvije paralelne prave razmaka h(a).Neka je na jednoj vrh C (odaberi proizvoljno) i u njoj leži stranica a.U drugoj leži vrh A.(Naći ćemo ga kasnije.)
2)Napravi simetralu na h(a) na kojoj leže polovišta stranica c i b.(Ova prava leži između dvije prethodne tačno u sredini.A polovišta su na njoj zato što je centar opisane kružnice pravouglog trokuta uvjek na polovištu hipotenuze.)
3)Napravi polovište na c strani iz odabrane tačke C pomoću radijusa t(c).Nazovimo tu tačku D.
-Sad kreni od ekstremnog slučaja kada je stranica b upravo jednaka visini h(a) i tekuća tačka A tvori tu visinu AC.Preostali dio dužine (a+b) je na pravcu koji sadrži stranicu a.Dakle to tekuće a je duž CB.Primjetimo da tačke ADB ne moraju ležati na istom pravcu.
-Zato potegnimo tačku A duž njenog pravca pri čemu će se stanica b povećavati a stranica a smanjivati sve dok ADB ne legnu na zajednički pravac.
-Ovim je konstrukcija trougla završena, a na nama je da izračunamo kolika je bila dužina (s) tog potezanja tačke A do A .To mora biti izraženo pomoću veličina: visine,težišnice i sume a+b.
-Radi manje zabune priložiću skicu (čim je nacrtam),a račun neću jer je lako izvodiv .Ispada po meni da je za geometrijsku konstrukciju potrebna sprava za crtanje elipse,dakle nisu dovoljni lenjir I šestar.

Ipak evo i računa.

Algebarski izraz za izračunavanje s:

_{[Ovu poruku je menjao zzzz dana 13.10.2015. u 10:52 GMT+1]}

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

ZZ12.10.JPG

ZZ12.10.JPG - 11.86k

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
*.vs.rs.

+391 Profil

Re: Aksiome geometrije i izvodjenje

^{13.10.2015. u 11:53 - pre 116 meseci}

Milane, traži se klasična konstrukcija.
Zadatak je iz Geometrije.

Evo i link:
https://imi.pmf.kg.ac.rs/moodl...jumi/Geom_prvi_kolokv_2011.pdf

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.customer.blic.net.

+197 Profil

Re: Aksiome geometrije i izvodjenje

^{13.10.2015. u 23:41 - pre 116 meseci}

Meni se ovaj zadatak preslikava u elipsu kojoj je e = t_c;2a=a+b
.a tu elipsu sječe pravac koji prolazi kroz jednu žižu i prolazi pored druge žiže na udaljenosti h_a.Treba naći presječnu tačku.Nebih znao to uraditi šestarom i lenjirom.
Ajmo pitati autore na ovoj adresi: [email protected]

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.customer.blic.net.

+197 Profil

Re: Aksiome geometrije i izvodjenje

^{14.10.2015. u 13:31 - pre 116 meseci}

Citat:

Evo resenja:

Konstruise se duz CD=a+b=d. Povuce se prava p paralelna sa pravom CD na odstojanju h_a. Iz tacke C se opise krug sa centrom C i poluprecnika 2m_c. Presek tog kruga i prave p je tacka E. Neka je F srediste duzi CE. Spojimo B i F.

Prava BF sece pravu p u tacki A, cime je konstruisan trougao ABC.

Ideja je da se produzi tezisna duz m_c, I da se na tu duz nadoveze jos jedna tezisna duz. Tako nastaje parallelogram BCAE, gde je CE=2m_c. Zatim se duz BE=b nanese na pravu BC, I tako se dobije duz BD=BE. Tada je CD=BD+BC=a+b.

Nadam se da cete razumeti resenje.

Puno pozdrava,

Prof. Emilija

Ovdje nedostaje način dobijanja tačke B što nije teško zaključiti.To je presjek duži CD i simetrale duži ED.
Zahvaljujemo se prof.Emiliji Nešović.Evo i skice tog gješenja.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

ZZ14.10..JPG

ZZ14.10..JPG - 8.34k

Odgovor na temu

[es] :: Matematika :: Aksiome geometrije i izvodjenje

Strane: 1 2

[ Pregleda: 5897 | Odgovora: 21 ] > FB > Twit

Srodne teme

15.03.2009. Potrebna pomoc oko ispita
09.06.2009. elektronstalacije
01.06.2009. elektroinstalacije
26.02.2010. nacrtna geometrija
14.04.2011. Elipticka geometrija
13.11.2012. Metrički prostori - interesantan zadatak
02.11.2013. Osnovni stav algebre
26.01.2014. Nesto iz analiticke geometrije
27.02.2015. Problem iz geometrije, hitno

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.