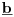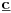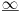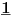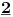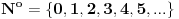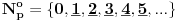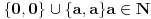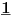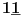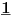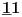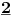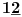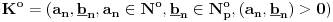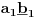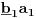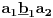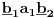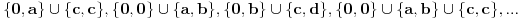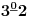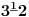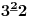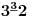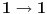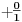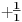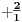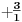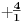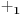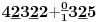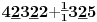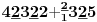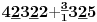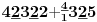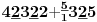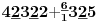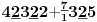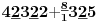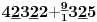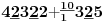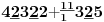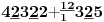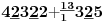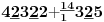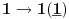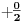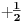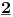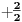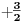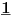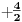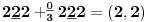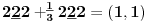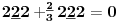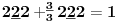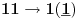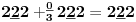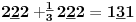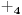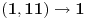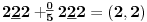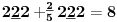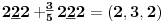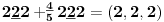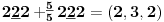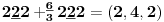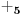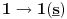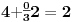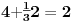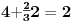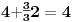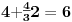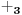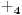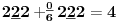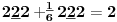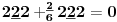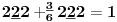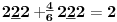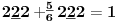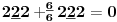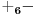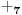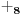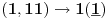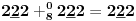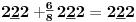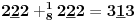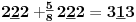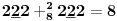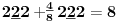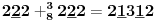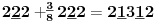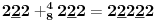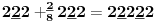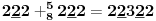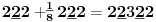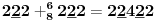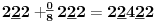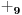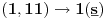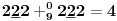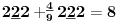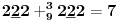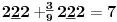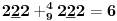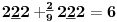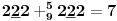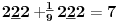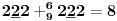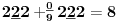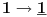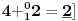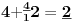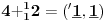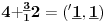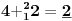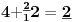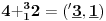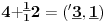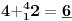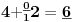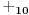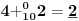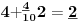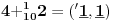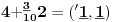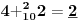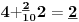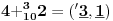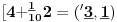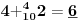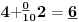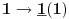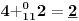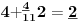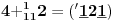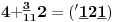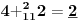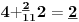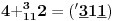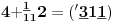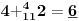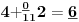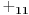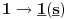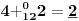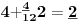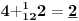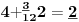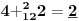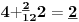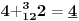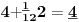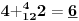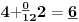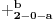[es] - matematika po srđanu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

^{28.04.2015. u 14:01 - pre 122 meseci}

Prestaviću vam matematiku sastavljenu od samo dva osnove ( prirodna i realna osnova ) .

Sadašnja matematika ( SM. )

PRIRODNA OSNOVA
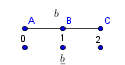
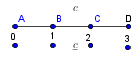
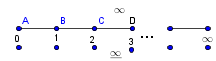
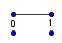
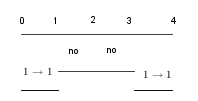
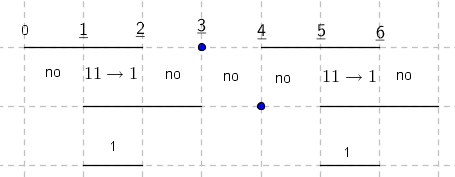
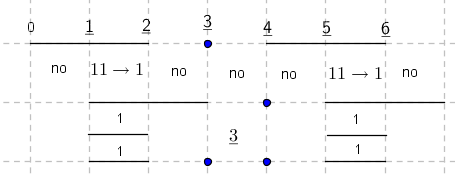
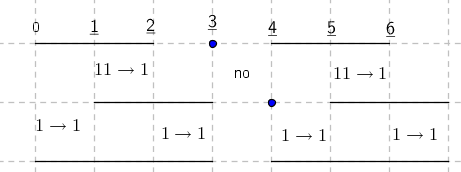
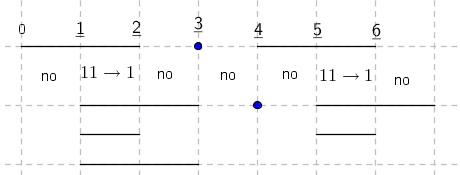
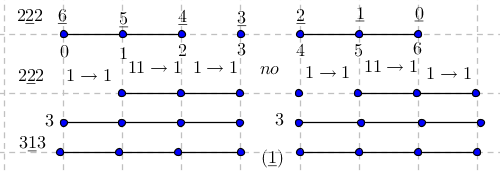
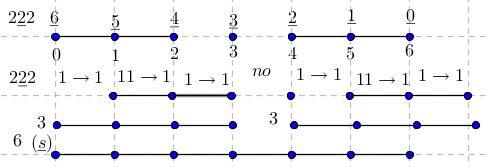
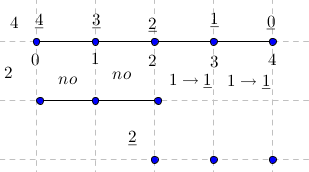
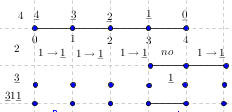
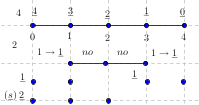
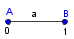
-prirodna duž je osnovni aksiom , njen početak ili kraj je tačka , prirodna duž je definisana dužinom i sa dve tačke
NOTACIJA - prirodna duž ( malim slovima ) , tačka ( velikim slovima ili brojevima ( kada su navedeno tačke postavene metrički ( kao na brojevnoj pravi )))

-prirodna praznina je negacija prirodne duži , prirodna praznina je definisana prazninom i sa dve tačke
NOTACIJA - prirodna praznina ( malim podvućenim slovima )

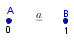
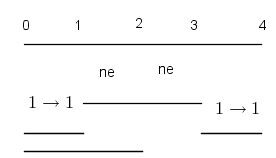
-osnovno pravilo spajanja - prirodne duži i prirodne praznine se spajaju samo tačkama
-osnovni skup - sve mogućnosti definisane teoremom
(SM.) - ne poznaje prirodnu duž , tačka nije definisana , ne poznaje prirodnu prazninu , nije definisan skup

Prikačeni fajlovi

m (1).png - 5.01k

mm.png - 4.08k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{29.04.2015. u 07:48 - pre 122 meseci}

TEORTEMA - Prirodne duži ( prirodne praznine ) se spajaju u smeru tačaka AB ( 0,1)

DOKAZ- duž ( praznina ) b (

) definisana AC ( 0,2)

duž ( praznina ) c (

) definisana AD ( 0,3)

...
beskonačna jednosmerna duž ( beskonačna jednosmerna praznina )

(

) definisana A

(0,

)

(SM.) - duž postoji ( ne iz prirodne osnove ) , praznina ne postoji , jednosmerna beskonačna duž ( polu-prava ( ne iz prirodne osnove )) , jednosmerna beskonačna praznina ne postoji

_{[Ovu poruku je menjao point.ms dana 30.04.2015. u 14:35 GMT+1]}

Prikačeni fajlovi

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{30.04.2015. u 13:33 - pre 122 meseci}

TEOREMA - postoji odnos između tačke 0 i svih tačaka na jednosmernu beskonačnu duž ( jednosmernu beskonačnu prazninu ) uključujuću i tačku 0

DOKAZ- odnos tačke 0 i tačke 0 je broj 0

-odnos tačke 0 i tačke 1 je broj 1(

)

--odnos tačke 0 i tačke 2 je broj 2(

)

...

osnovni skup prirodnih brojeva

osnovni skup prirodnih praznina brojeva

(SM.) - prirodni brojevi su dati kao aksiom , ne postoji prirodni praznina brojeva ( postoji ovaj oblik ,ali se ne zovu brojevi (

)

Prikačeni fajlovi

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{01.05.2015. u 10:15 - pre 122 meseci}

TEOREMA - prirodni brojevi i prirodni praznina brojevu se mogu spajati u smeru AB ( 0,1 )

DOKAZ - broj 1 i broj

dobija se kombinovani broj

ili dup ( duž , praznina )

- broj

i broj 1 , dobija se kombinovani broj

ili dup

- broj 1 i broj

, dobija se kombinovani broj

ili dup

...
- osnovni skup kombinovanih prirodnih brojeva

...

(SM.) - ne poznaje dup , ne poznaje kombinovane brojeve ( postoji ovaj oblik , ali nisu brojevu

)

Prikačeni fajlovi

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{02.05.2015. u 10:33 - pre 122 meseci}

TEOREMA - Dva broja imaju kontakt , njihovo stanje se opisuje tačkama prvog broja

DOKAZ - broj 3 i broj 2 imaju kontakt u tački 0

- broj 3 i broj 2 imaju kontakt u tački 1

- broj 3 i broj 2 imaju kontakt u tački 2

- broj 3 i broj 2 imaju kontakt u tački 3

(SM.) - ne poznaje kontakt brojeva

Prikačeni fajlovi

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{03.05.2015. u 11:22 - pre 122 meseci}

TEOREMA - U kontaktu brojeva sortira se horizontalno da bude samo jedna prirodna duž koja daje prirodnu duž

DOKAZ -

2=2

4

2=(1,1)

4

2=2

4

2=(3,1)

4

2=6 ili 4+2=6

- sabiranje pravilo 1

(SM.) - ne poznaje "sabiranje pravilo 1 " , samo kada je kontakt brojeva tačkom , aksiom
dobili smo prvi oblik sabiranja , prednost moje matematike
-----------

pitanje za školovane matematičare ,koji je postupak treba primeniti da bi se dobili ( znak ? )
4 ? 2=2
4 ? 2=(1,1)
4 ? 2 =2
4 ? 2=(3,1)
4+2=6 to je poznato
malo složenije
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (1,1,1,2) moje rešenje i notacija

=(1,1,1,2)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (1,4) moje rešenje i notacija

=(1,4)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (2,1,1,2,1) moje rešenje i notacija

=(2,1,1,2,1)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (3,4,2) moje rešenje i notacija

=(3,4,2)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (6,4,1) moje rešenje i notacija

=(6,4,1)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,1,1,1,2) moje rešenje i notacija

=(4,1,1,1,2)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,3) moje rešenje i notacija

=(4,3)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,1,1,4) moje rešenje i notacija

=(4,1,1,4)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,2,2,5) moje rešenje i notacija

=(4,2,2,5)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,5,5) moje rešenje i notacija

=(4,5,5)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,3,1,5) moje rešenje i notacija

=(4,3,1,5)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,3,1,5) moje rešenje i notacija

=(4,3,1,5)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,3,2,5) moje rešenje i notacija

=(4,3,2,5)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,3,3,5) moje rešenje i notacija

=(4,3,3,5)
{0,4}

{6,9}

{11,13} ? {0,3}

{5,10} = (4,3,3,5) moje rešenje i notacija

=(4,3,3,5)

Prikačeni fajlovi

ccc.png - 0.66k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{05.05.2015. u 10:02 - pre 122 meseci}

TEOREMA - U kontaktu brojeva sortira se horizontalno da bude samo jedna prirodna duž koja daje prirodnu duž , kada ima dva ( više ) rezultata između njih postaje praznina .

DOKAZ -

2=2

4

2=1

1

4

2=2

4

2=3

1

4

2=6

+₂ - sabiranje pravilo 2

(SM.) - ne poznaje "sabiranje pravilo 2 "

Prikačeni fajlovi

ccc1.png - 0.85k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{06.05.2015. u 08:31 - pre 122 meseci}

Teorema - u kontaktu brojeva , vrši se horizontalno sortiranje , dve prirodne duži daju jednu prirodnu duž

Dokaz-

- sabiranje pravilo 3

(CM.) - Ne " sabiranje pravilo 3"

Prikačeni fajlovi

yy.png - 4.85k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{07.05.2015. u 17:47 - pre 122 meseci}

Teorema - u kontaktu brojeva , vrši se horizontalno sortiranje , dve prirodne duži daju jednu prirodnu duž , kada ima dva ( više ) rezultata između njih postaje praznina .

Dokaz-

- sabiranje pravilo 4

(SM.) - Ne " sabiranje pravilo 4"

Prikačeni fajlovi

yy1.png - 5.26k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{10.05.2015. u 18:14 - pre 122 meseci}

Teorema - u kontaktu brojeva , vrši se horizontalno sortiranje , samo jedna prirodna duž daje prirodnu duž i dve prirodne duži daju jednu prirodnu duž

Dokaz-

- sabiranje pravilo 5

(SM.) - Ne " sabiranje pravilo 5"

Prikačeni fajlovi

yy2.png - 4.81k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{11.05.2015. u 16:10 - pre 122 meseci}

TEOREMA - U kontaktu brojeva sortira se horizontalno da bude samo jedna prirodna duž koja daje prirodnu duž , kada ima dva ( više ) rezultata oni se spajaju

DOKAZ -

- sabiranje pravilo 3

(SM.) - ne poznaje "sabiranje pravilo 3 "

NAPOMENA , pređašnje

postaje

, pređašnje

postaje

Prikačeni fajlovi

cccc.png - 1.1k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{14.05.2015. u 08:27 - pre 121 meseci}

Teorema - u kontaktu brojeva , vrši se horizontalno sortiranje , dve prirodne duži daju jednu prirodnu duž , kada ima dva ( više ) rešenja se spajaju.

Dokaz -

sabiranje pravilo 6

(SM.) - ne poznaje "sabiranje pravilo 6 "

NAPOMENA , pređašnje

postaje

Prikačeni fajlovi

www.png - 4.75k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{18.05.2015. u 07:36 - pre 121 meseci}

sa ispravljenim greškama na PDF

https://onedrive.live.com/redi...P--a4Vsc&ithint=file%2cpdf

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{23.05.2015. u 13:00 - pre 121 meseci}

TEOREMA - U kontaktu brojeva sortira se vertikalno:
- samo jedna prirodna duž daje prirodnu duž
- dve prirodne duži koja daje prirodnu duž
- kada ima dva ( više ) rešenja između njih postaje praznina
DOKAZ -

ili

- sabiranje pravilo 8

(SM.) - Ne " sabiranje pravilo 8"

Prikačeni fajlovi

1.png - 8.98k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{25.05.2015. u 10:19 - pre 121 meseci}

TEOREMA - U kontaktu brojeva sortira se vertikalno da bude samo jedna prirodna duž daje prirodnu duž
- dve prirodne duži koja daje prirodnu duž ,
- kada ima dva ( više ) rešenja između njih , se spajaju
DOKAZ -

ili

- sabiranje pravilo 9

(SM.) - Ne " sabiranje pravilo 9"

Prikačeni fajlovi

y4.png - 27.01k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{26.05.2015. u 09:04 - pre 121 meseci}

TEOREMA - U kontaktu brojeva sortira se vertikalno da bude samo jedna prirodna duž koja daje prirodnu prazninu

DOKAZ

ili

- sabiranje pravilo 10

(SM.) - ne poznaje "sabiranje pravilo 10 "

Prikačeni fajlovi

y5.png - 4.11k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{30.05.2015. u 13:44 - pre 121 meseci}

GREŠKA - u predhodnom postu treba ovako

ili

TEOREMA - U kontaktu brojeva sortira se vertikalno da bude samo jedna prirodna duž koja daje prirodnu prazninu
-kada ima dva ( više ) rešenja između njih postaje duž

DOKAZ -

ili

- sabiranje pravilo 11

(SM.) - ne poznaje "sabiranje pravilo 11 "

Prikačeni fajlovi

8.png - 3.89k

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{03.06.2015. u 10:42 - pre 121 meseci}

TEOREMA - U kontaktu brojeva sortira se vertikalno da bude samo jedna prirodna duž koja daje prirodnu prazninu
-kada ima dva ( više ) rešenja oni se spajaju

DOKAZ -

ili

- sabiranje pravilo 12

(SM.) - ne poznaje "sabiranje pravilo 12 "

Prikačeni fajlovi

1.png - 8.98k

Odgovor na temu

pexxi92

Član broj: 291395
Poruke: 49
*.dynamic.isp.telekom.rs.

+25 Profil

Re: matematika po srđanu

^{08.06.2015. u 14:10 - pre 121 meseci}

Jel tebi dobro?

Odgovor na temu

point.ms
ne radim
ne radim

Član broj: 327434
Poruke: 49
176.104.110.*

Profil

Re: matematika po srđanu

^{07.10.2015. u 18:03 - pre 117 meseci}

https://onedrive.live.com/redi...mPAQIBxU&ithint=file%2cpdf

, pošto sam otkrio nove oblike sabiranja , 2 ( može biti n ( n>2)) , 0 ( vertikalno sortiranje , kada je nD ili nL onda je kososortiranje ) , a oblik sabiranja .

pozivam sve forumaše da moje izlaganje prikažu rešenja sa znanjem sadašnje matematike ( osnova je prilog na pdf )

Odgovor na temu