Hajde da dam hint za drugi.
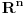
se može predstaviti kao prebrojiva disjunktna unija slika skupa
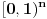
pri translacijama. Dakle, treba problem rešiti za slučaj Lebegove mere na njima.
Ako je neki prostor snabdeven sigma aditivnom merom u kojoj su tačke mere nula, onda je taj prostor izomorfan prostoru koji se od tog dobija izbacivanjem najviše prebrojivog skupa tačaka.
Na skupu
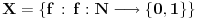
se može uvesti najmanja sigma aditivna kompletna mera koja ispunjava sledeći uslov: Za svaki izbor različitih prirodnih brojeva

i izbor vrednosti
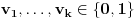
je mera skupa
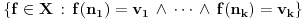
je jednaka
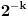
. Ona se može shvatiti i kao normiana mera na Kantorovom skupu (dakle, ne nasleđena od Lebegove) u kojoj podudarni delovi imaju istu meru, a skup tačaka Kantorovog skupa druge vrste je izomorfan sa

sa izbačenim tačkama oblika
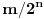
snabdevenim Lebegovom merom. Idempotentnost od

se kudikamo lakše dokazuje.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
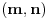 takve da su grupe
takve da su grupe 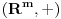 i
i 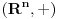 izomorfne.
izomorfne.