Ova suma
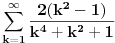
se moze naci vrlo lako. Ponekad ne treba bespotrebno petljati. Naravno, resenje je parcijalna dekompozicija izraza pod sumom. Naime,
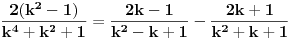
. Primetimo da je
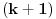
-vi clan oblika
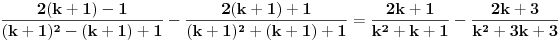
, tj. primecujemo pravilo kako se uzastopni clanovi u datoj sumi skracuju. Sada lako nalazimo da je
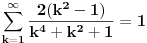
.
I neko bi sad rekao, odlicno, nasli smo polaznu sumu
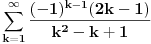
. E pa, prc, nismo, jer ne vazi
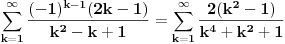
, ja sam pogresio u racunu tada. Naime, ideja razdvajanja na parove
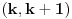
se ne moze primeniti tako da suma ostane da ide od
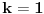
do

. Moze da se razdvoji ali tako da indeksi idu po neparnim brojevima
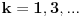
, onda bi bilo korektno, ali bi bilo zeznuto naci tu sumu. Ako bismo rastavili na parne i neparne clanove, dakle, oblika
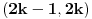
, onda bi

islo lepo redom, ali bismo dobili komplikovaniju sumu, naime, tada bi vazilo
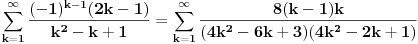
. Ali, treba ovo izracunati.
Al ako nista, za utehu, na ovaj nacin smo nasli sumu
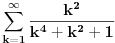
. Iz prethodnih razmatranja nalazimo
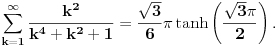
Ali uspeo sam da izracunam i pocetnu sumu, polazeci od pocetne sume
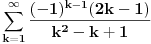
(dakle, sve ove modifikacije mi nisu bile od nekog veceg znacaja). Naime, iz mog prethodnog posta nalazimo
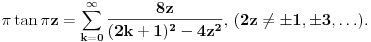
Iz transformacije
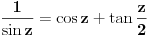
nalazimo dalje
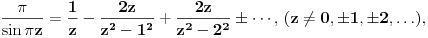
a zamenjujuci

sa
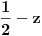
nalazimo
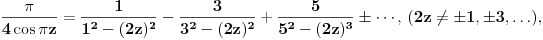
odnosno

.
Ovde je prakticno kraj, jer stavljajuci
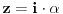
nalazimo
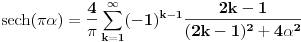
, a zatim stavljajuci
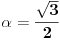
nalazimo
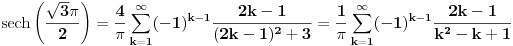
, odnosno
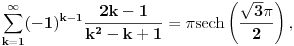
sto je i trebalo naci.
Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.