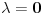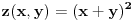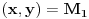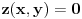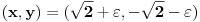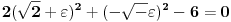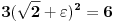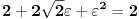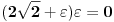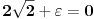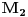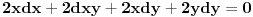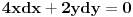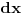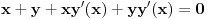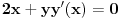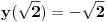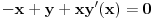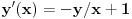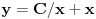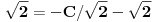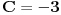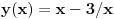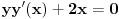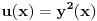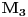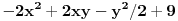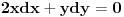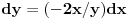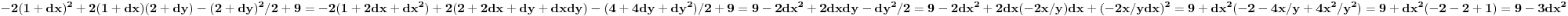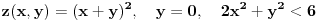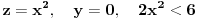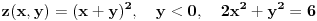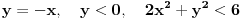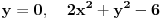Odrediti uslovni ekstremum funkcije
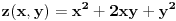 za
za 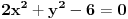 , a potom odrediti najmanju i najvecu vrednost na zatvorenoj oblasti
, a potom odrediti najmanju i najvecu vrednost na zatvorenoj oblasti 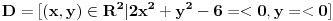 .
.Formirao sam Lagranzovu funkciju i nasao
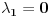 i
i 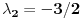 gde su za
gde su za 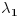 stacionarne tacke
stacionarne tacke 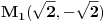 i
i 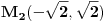 , a za
, a za 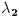 su
su 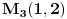 i
i 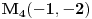
Posle nadjem totalni diferencijal drugog reda ali imam poteskoce da odredim znak, pokusao sam pre toga Silvesterovom teoremom naravno bez uspeha.
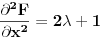
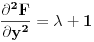
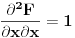
I jedno pitanje. Za drugi deo zadatka kada trazim najm. i najv. vred. na zatvorenoj oblasti, prilikom postupka kada prvo nadjem stacionarne tacke funkcije z(x,y) treba da proverim da li pripadaju toj oblasti?
EDIT:
Uspeo sam, trebalo je jos da nadjem diferencijal uslova, pa su
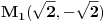 i
i 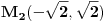 minimumi, a
minimumi, a 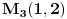 i
i 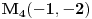 maksimumi. Dalje za zatvorenu oblast dobijam i
maksimumi. Dalje za zatvorenu oblast dobijam i 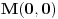 , kojoj pripadaju i
, kojoj pripadaju i 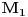 i
i 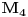 . Sledi da je najmanja vrednost u M gde je z=0, a najveca u
. Sledi da je najmanja vrednost u M gde je z=0, a najveca u 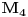 gde je z=9.
gde je z=9.Nadam se da ce jos neko da potvrdi moje resenje...
[Ovu poruku je menjao nightowl dana 04.11.2012. u 01:23 GMT+1]
[Ovu poruku je menjao nightowl dana 04.11.2012. u 01:24 GMT+1]




 Uslovni ekstremum
Uslovni ekstremum