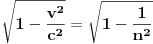Vratimo se naslovu teme ovim tekstom iz udžbenika o STR:
U udžbeniku Fizičkog fakulteta Univerziteta u Beogradu „Specijalna teorija relativnosti“ II izdanje iz 1997 god autor (Vida J. Žigman) u poglavlju 2.3.2 – „Poređenje merenja dužina u pravcu relativnog kretanja“ piše:
Najjednostavnije izvođenje kontrakcije dužina koristi upravo rezultata dilatacije vremena, direktno pokazujući da je kontrakcija dužina nužna posledica dilatacije vremena.
Zamislimo dva posmatrača, pri čemu jedan sedi u vozu koji se kreće kroz stanicu konstantnom brzinom v (sistem reference S'), a drugi miruje na stanici (sistem reference S). Oba posmatrača mere dužinu platforme na stanici, znajući da intenzitet njihove relativne brzine iznosi v. Posmatrač na zemlji meri vremenski interval ∆t između putnikovog prolaska tačke početka i tačke kraja platforme. Vreme ∆t je nesopstveno vreme jer se meri između dva događaja koji se dešavaju na različitim mestima (putnik prolazi tačku početka i putnik prolazi tačku kraja platforme), tj na dva različita časovnika. Posmatrač na zemlji konstatuje da je dužina platforme L = v∆t. Međutim, putnik iz voza opaža da se platforma prvo približava, a zatim udaljava od njega. On beleži, na primjer na svom ručnom časovniku, trenutak kada početak platforme „prolazi“ pored njega i zatim trenutak kada kraj platforme „prolazi“ pored njega. Za njega (S'), ta dva događaja se dešavaju na istom mestu. Vremenski interval između njih on meri jednim časovnikom (ručnim satom) na jednom mestu koje koincidira sa mestom dešavanja dva događaja. Putnik, dakle, meri sopstveni vremenski interval ∆t', i za njega je dužina platforme L' = v∆t'. Vremenski intervali ∆t i ∆t' povezani su, kao što smo videli iz prethodnog primera, relacijom
∆t' = ∆t√(1-β2).
Dužine platforme merene sa stanovišta putnika u vozu (L') i posmatrača na zemlji (L) odnose se kao odgovarajući mereni vremenski intervali ∆t i ∆t', odnosno L'/L = ∆t'/∆t, što prema prethodnoj relaciji daje:
L' = L√(1-β2) .
Dolazimo do rezultata kontrakcije dužina: Telo sopstvene dužine L (platforma miruje u sistemu zemlje, S), paralelne pravcu relativnog kretanja, ima dužinu L√(1-β2) u sistemu u odnosu na koji se kreće brzinom v (platforma se kreće u sistemu putnika, S').
-----------------------------
"Eksperimentišite" malo sa konkretnim brojnim vrijednostima veličina! Osmislite neko n = c/v kako bi nam dužine ("kontrakcije") bile "vidljive". Predlažem n = 5/3 (koje najčešće koristim na crtežima), ili n = 4/3 ("vakum"/"voda"), ili n = 5/4 . Tko želi računati sa veličinama u MM eksperimentu neka koristi n = 10
4.
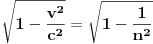
. Formulu sam "zalijepio" kako bih ponovo skrenuo pažnju da vrijednost "relativističkog faktora" ne zavisi od skalarnih vrijednosti ( od intenziteta) brzina c i v , n = c/v > 1).
Izračunavanja tačnih (ne približnih) vrijednosti veličina (ct, vt, ct
1, vt
1, ct
2 , vt
2 , osim 2ct' i 2vt') u Majkelson-Morlijevom eksperimentu moguće je ako umjesto PO = 11m (već sam rekao da je i ova veličina sporna - PO u Majkelsonovom interferometru nije iznosilo 11 m, kako to tvrde "sastavljači proračuna" i tvorci "očekivanog rezultata", već "mnogo manja" - "mnogobrojne refleksije" ne povećavaju razliku ct - 2l
0 iz "prve refleksije") koristimo još, skoro pet puta, veću dužinu PO = 49,9999995m. Kako su obje veličine ct i 2ct' direktno proporcionalne dužini PO to će i razlika ct – 2ct' biti skoro pet puta veća. Međutim, i za ovoliko povećanu razliku ta razlika je po veličini skoro identična talasnoj dužini korištene svjetlosti (λ
0 = 0,59·10
-6 m). U to se možete uvjeriti i iz upoređivanja ct – 2l
0 > ct – 2ct' , jer je 2ct' > 2l
0 . Sada se mogu iskazati tačne brojne vrijednosti veličina (bez zaokruživanja) ct = 100m, i 2l
0 = 99,999999m, i utvrditi tačna razlika ct - 2l
0 = 1·10
-6 m.
[Ovu poruku je menjao Sprečo dana 16.04.2012. u 18:54 GMT+1]




 Re: Paradoks kontrakcije
Re: Paradoks kontrakcije