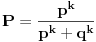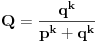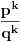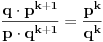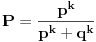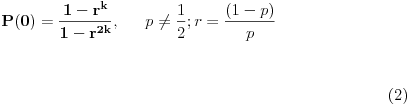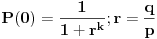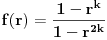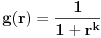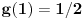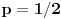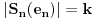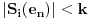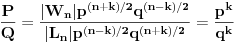Srodne teme

03.10.2007. MATURSKI - Informacioni sistemi
17.03.2004. Presek elipsoida i poluprave !?!?
11.07.2006. Access - problem oko racunanja stanja lagera
18.06.2005. Pitanj(c)e iz verovatnoce?
20.06.2006. Kako sadrzaj Edit-boxa pretvoriti u numericku pro..
11.12.2013. [Excel] Zaokruzivanje kod racunanja procenata u t..
07.01.2007. [Excel] problemcic oko racunanja datuma
23.02.2007. Pomoc oko racunanja vrednosti
29.03.2007. Problem u matlabu sa obradom zvuka
17.03.2008. Pomoc oko racunanja dana npr od 13.01.2005 pa do ..

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Problem oko teorijskog racunanja verovatnoce

[es] :: Matematika :: Problem oko teorijskog racunanja verovatnoce

Strane: 1 2

[ Pregleda: 7286 | Odgovora: 38 ] > FB > Twit

Autor

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.41.*

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{22.01.2012. u 11:03 - pre 174 meseci}

Pa, ja sam odustao jer mi se cini sve to previse komplikovano :) Probao sam da resim na neki drugi nacin, ali sam se zaglavio a nemam previse vremena da se bavim time.
Zadatak izgleda uopste nije naivan; ideja mi je bila da posmatram skupove pobeda u klasama duzine n; hocu reci, klasa bi bila skup svih pobeda u n >=k koraka.
Tu se lako vidi da je broj pogodaka (n+k)/2 a promasaja (n-k)/2; takvi skupovi pobeda su disjunktni pa bi se verovatnoca sabirala.
Verovatnoca svake pobede u n pokusaja je

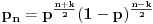Problem je nastao kada sam pokusao da odredim koliko ima elemenata takva klasa, tj. na koliko nacina se moze pobediti u n koraka. Ako bih to nasao, npr neko c_n, onda bi valjda ukupna verovatnoca biila

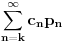. A kako nisam uradio ni ovaj prvi deo, nemam pojma sta bi me sacekalo sa ovim redom :)

U svakom slucaju, posto to nisam uspeo da isteram do kraja, mogu samo da se slozim sa Nedeljkom za koga sam siguran da se dovoljno potrudio oko analize zadatka.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{22.01.2012. u 11:16 - pre 174 meseci}

@Nedeljko

Pravo da ti kažem tu poruku nisam ni čitao do kraja zbog onog "Hihihi!". Posebno kad si kasnije uveo "indikator". A i da sam "prepisao" početne uslove trebalo je izračunati verovatnoću bez pretpostavke o "indikatoru" jer bilo bi neoprezno od mene da prepisujem nešto što sam osporio.

To jedno, a drugo, koristio sam formulu za verovatnoću pogotka prvim hicem, koju sam upravo ja prvi napisao. Ta formula stoji. Naravno, ja mogu sad da spekulišem da si ti prepisao od mene.

A što se tiče verovatnoće dogadjaja da je sakupljeno k poena te formule i dalje stoje. Još jednom, kao šro sam ranije napisao, to nije verovatnoća pobede. No ako ti misliš da je formula za izračunavanje "verovatnoće dogadjaja da je sakupljeno k poena" nije tačna niko ti ne brani da je izračunaš.

Ti i dalje braniš nešto što je neodbranjivo (pretpostavka o indikatoru) i da bi to maskirao napadaš nešto što niko ne brani. Jeste, napisao sam to što sam napisao i ja to ne sporim. Ono što sporim je kontekst koji si ti izvrnuo i sad ponavljaš "ko švaba tralalala" da sam nešto napisao. Da sam ćutao (kao što ti ćutiš o indikatoru) imao bi osnova da ponovo citiraš poruku. Pa objasnio sam u kom kontekstu sam napisao i nemoj se više truditi da promeniš kontekst (stalnim zvocanjem) već olovku u šake i izračunaj da li je tačno to što sam izračunao (ali u onom kontekstu kako sam napisao a ne tvoje zamene konteksta).

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.

+2807 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{22.01.2012. u 16:03 - pre 174 meseci}

darkosos

Ako ti ne ide na taj način, zašto ne probaš na drugi? Reci šta ti konkretno nije jasno u mom rešenju, pa ću pokušati da ti objasnim.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.dynamic.isp.telekom.rs.

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{23.01.2012. u 07:39 - pre 174 meseci}

Hvala ti Nedeljko, ali mene pre svega interesuje otkud ti ideja da na takav nacin resavas? :)
MIslim, nije bas tako ocigledno, ici preko uslovne verovatnoce za pobedu ako imas i poena... Mozda je to neka klasa problema u koju ovo upada?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.

+2807 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{23.01.2012. u 13:11 - pre 174 meseci}

Pa, bio je neki sličan, ali ne isti zadatak sa pijancem koji stoji na litici i samo što ne padne, pašće ako napravi samo jedan korak napred (odmah), a pravi nasumične korake napred i nazad iste dužine. Takođe, ovaj zadatak se za k=2 svodi na to koji će teniser da osvoji gem pri rezultatu 40:40, o čemu sam već razmišljao.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{23.01.2012. u 14:02 - pre 174 meseci}

Rekao bih da su u pitanju lanci Markova.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.

+2807 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{23.01.2012. u 15:35 - pre 174 meseci}

Jesu lanci Markova, ali to treba dokazati. Dao sam ideju kako.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.rs.

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{24.01.2012. u 12:46 - pre 174 meseci}

Evo sta sam nasao na ovu temu: http://en.wikipedia.org/wiki/Random_walk

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2168
..able.dyn.broadband.blic.net.

+197 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{24.01.2012. u 16:09 - pre 174 meseci}

Ovaj zadatak je sasvim jednostavan i može se odmah intuitivno riješiti.

Vjerovatnost pobjede P je:

,a poraza Q je:

,(p je šansa pogotka,q je šansa promašaja (p+q=1),a k je zadana razlika između broja pogodaka i promašaja.)

Dokaz intuitivnog rješenja:
Ako pođemo od tvrdnje da će razlika (kad tad) između pogodaka i promašaja biti k,(a ima dokaz za to!),onda slijedi:

-Ako se to desilo u k-tom pokušaju (a ranije nije ni moglo),onda je omjer između mogućnosti da je tada pobjedio ili izgubio jednak:

,a šansa da je u takvom slučaju to baš bila P je :

-Ako se to desilo u k+2-tom pokušaju ,onda je omjer između mogućnosti da je tada pobjedio ili izgubio jednak:

,a šansa da je pobjedio je:

-Itd za svako k+2i (ako se desila razlika k) imamo isti omjer šansi .Pa ako će se to desiti u ko zna kom potezu šansa je ostala ista .

(Formula koju je napisao kanduros je ispravna samo nesređena,i izvedena na komplikovan način koji mi obični ne razumijemo.)

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.

+2807 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{24.01.2012. u 18:41 - pre 174 meseci}

Bravo zzzz!

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{24.01.2012. u 23:14 - pre 174 meseci}

Citat:

Formula koju je napisao kanduros je ispravna samo nesređena,i izvedena na komplikovan način koji mi obični ne razumijemo.

A ja se "satra" da ispišem što jednostavnije da svi ukapiraju.

_{[Ovu poruku je menjao kandorus dana 25.01.2012. u 10:16 GMT+1]}

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.dynamic.isp.telekom.rs.

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{25.01.2012. u 07:39 - pre 174 meseci}

Sjajno zzzz, i mene je bolela glava :) Jos samo treba dodati, da zbog toga sto trazis razliku k, mora biti P+Q=1, odakle verovatno i izvodis formulu za P (imas P/Q i P+Q, pa kao sistem jednacina). Ja sam se tu malo zabunio, pa zato kazem...

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2168
..able.dyn.broadband.blic.net.

+197 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{25.01.2012. u 21:51 - pre 174 meseci}

Citat:

kandorus: A ja se "satra" da ispišem što jednostavnije da svi ukapiraju.

Mislio sam na:

@kandorus:verovatnoća pobede je:

,a moglo je ići kraćenje sa (1-r^k) Pa bi bilo:

, izbjegao bi dodatno "satiranje" za p=1/2 koje nije lako ukapirati.Ne ljutiš se valjda?

Citat:

Sjajno zzzz, i mene je bolela glava :) Jos samo treba dodati, da zbog toga sto trazis razliku k, mora biti P+Q=1, odakle verovatno i izvodis formulu za P (imas P/Q i P+Q, pa kao sistem jednacina).

Ja sam krenuo obrnuto.Ovako:Ako saznam da je strijelac završio gađanje,a ne znam kako je prošao,na šta bih se kladio?Pobjeda ili poraz?Kolika bi mi šansa bila da pogodim?I da li je važno znati u kom hicu se to desilo?Odgovore na ova pitanja lako je naći bez olovke i papira uz pivo u bučnoj kafani.Hvala vam na priznanjima,mada mislim da nema nekog razloga jer se ipak radi o jednostavnom problemu.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{25.01.2012. u 22:38 - pre 174 meseci}

Upppssss, za p=1/2 važi

1 - r^k = 1 - ((1-p)/p)^k =
= 1 - 1^k = 0

a deljenje nulom nije dozvoljeno.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2168
..able.dyn.broadband.blic.net.

+197 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{26.01.2012. u 08:00 - pre 174 meseci}

Izvini ne razumijem šta želiš reći.Možeš li nama običnim koji to ne razumijemo malo razjasniti?
Da li bi po tvom išlo naprimjer ovako:

,zbog a+b=0,"a deljenje nulom nije dozvoljeno."

A nipošto ovako:

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{26.01.2012. u 09:25 - pre 174 meseci}

Za izraz P/Q u svim tačkama za koje izraz Q uzima vrednost nula nije dozvoljeno delenje. U ostalim tačkama je dozvoljeno pa za taj izraz M upravo tako se i piše, M = a - b, a <> b.

Kad je u pitanju odredjivanje izraza za verovatnoću, u navedenom zadatku, samo je u mom rešenju razmotren slučaj p = 1/2. Rešenje bi bilo nepotpuno ako se taj slučaj ne razmotri jer bi tada došlo do delenja nulom kao što sam već objasnio,

E sad, ako ti i dalje nije jasno onda ne znam šta da kažem osim da zaključim da su moja objašnjenja iskomlikovana pa ne umem da prenesem ono što mislim. Čak ni Nedeljku nije jasno šta ja pišem te mi ponekad pripisuje da sam napisao ono što on misli a ne ono što piše. Kad njemu nije jasno kako će onda biti drugima? Pa ne znam, ne umem da budem jednostavniji (iako se "satra").

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.dynamic.isp.telekom.rs.

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{26.01.2012. u 09:35 - pre 174 meseci}

Funkcije

i

imaju razlicite domene;
ali posto je

a

, kada bi dodefinisali f za r=1, tako da je f(1)=1/2, takve dve funkcije jesu identicne, jer imaju isti domen i svuda jednake vrednosti.

Ovo sve posmatrano za r>=0.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.

+2807 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{26.01.2012. u 10:33 - pre 174 meseci}

kandorus je u pravu da bi u njegovo rešenje bilo nepotpuno bez posebnog razmatranja slučaja

jer je njegov postupak takav da bi se u tom računu pojavilo deljenje nulom.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.dynamic.isp.telekom.rs.

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{01.02.2012. u 08:03 - pre 174 meseci}

E, ja moram da dodam jos nesto :)
Rekao bih da verovatnoca da igrac dobije u k+2 poteza nije p^k+1q, vec "broj varijanti pobeda u k+2 poteza" * p^k+1q.
Srecom, sve ostaje isto, zato sto je i "broj varijanti poraza u k+2 poteza" isti broj kao onaj gore.
Ne mogu da izdrzim a da to ne pokazem :)

Dakle, ako je npr Wn skup pobeda u n koraka a Ln skup poraza u n koraka, treba pokazati da je |Wn|=|Ln|. Ovo moze da se izvede koristeci funkciju f(en) = -en koja urejdenu n-torku iz {-1,1}ⁿ slika u isti taj skup tako da pomnozi svaku koordinatu sa -1, tj. pretvori promasaj u pogodak i obrnuto. Pokazacu da na taj nacin f slika pobedu u poraz i obrnuto (sjajna stvar :).
Da bih prikazao osobine elementarnog dogadjaja, uvescu sumu Si(en) koja predstavlja sumu koordinata, tj. bodova prvih i elemenata uredjene n-torke en. Da bi en bio elementarni dogadjaj ove igre, mora biti

1.

2.

za i=1,..,n-1

Lako se vidi da je

pa je

za i=1,..,n odakle se vidi da i -e_n zadovoljava prethodna dva uslova.
Takodje, posto

znaci pobedu, a

poraz, ova funkcija zaista preslikava pobedu u poraz i obrnuto.

Ostaje da se pokaze jos da je f:Wn->Ln bijekcija. 1-1 jeste sigurno jer je to na {-1,1}ⁿ. Iz tog razloga je i |Wn| = |f(Wn)|. Posto je f(Wn) podskup Ln i f(Ln) podskup Wn, vazi:

. Pocetak i kraj su jednaki pa su i ovi u sredini.

Konacno,

_{[Ovu poruku je menjao darkosos dana 01.02.2012. u 09:23 GMT+1]}

_{[Ovu poruku je menjao darkosos dana 01.02.2012. u 09:30 GMT+1]}

Odgovor na temu

[es] :: Matematika :: Problem oko teorijskog racunanja verovatnoce

Strane: 1 2

[ Pregleda: 7286 | Odgovora: 38 ] > FB > Twit

Srodne teme

25.01.2009. Supremum funkcije
07.02.2009. Treba mi pomoć oko verovatnoće
17.05.2010. proracun vratila-problem ili ne
13.03.2009. Pomoc oko verovatnoce.....
02.05.2009. Zaokruzivanje prilikom racunanja - POMOC
26.03.2010. Problem oko racunanja prosjeka
17.09.2010. MATLAB kumulativna funkcija verovatnoce
27.02.2011. Paralelno racunanje pomocu HLSL - Problemi
30.06.2011. Praktican problem iz verovatnoce.

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.