Srodne teme

03.10.2007. MATURSKI - Informacioni sistemi
17.03.2004. Presek elipsoida i poluprave !?!?
11.07.2006. Access - problem oko racunanja stanja lagera
18.06.2005. Pitanj(c)e iz verovatnoce?
20.06.2006. Kako sadrzaj Edit-boxa pretvoriti u numericku pro..
11.12.2013. [Excel] Zaokruzivanje kod racunanja procenata u t..
07.01.2007. [Excel] problemcic oko racunanja datuma
23.02.2007. Pomoc oko racunanja vrednosti
29.03.2007. Problem u matlabu sa obradom zvuka
17.03.2008. Pomoc oko racunanja dana npr od 13.01.2005 pa do ..

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Problem oko teorijskog racunanja verovatnoce

[es] :: Matematika :: Problem oko teorijskog racunanja verovatnoce

Strane: 1 2

[ Pregleda: 5907 | Odgovora: 38 ] > FB > Twit

Autor

beyn
Branko Popovic
Student
Beograd

Član broj: 261796
Poruke: 4
*.dynamic.isp.telekom.rs.

+2 Profil

Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 15:21 - pre 162 meseci}

Pozdrav svima.
Potrebna mi je mala pomoc oko racunanja verovatnoce. Naime problem je sledeci:

Igrac A gadja u metu (igru pocinje sa 0 poena) . Za pogodak dobija +1 poen a za promasaj -1 poen. Igrac je pobedio ukoliko osvoji k poena a partija je izgubljena ukoliko osvoji -k poena.
Znajuci verovatnocu pogotka p i broj poena koji treba da se osvoji k odrediti verovatnocu da ce igrac A da pobedi.

Ja sam ovaj problem resio preko programcica koji sam napravio. Jenostavno se unosi verovatnoca pogotka i broj poena koji treba osvojiti, zatim se simulira 10000 igara i krajnja verovatnoca se dobija kao broj_pobedjenih_igara\10000 i to fino radi,
Sada imam zadatak da izracunam istu tu verovatnocu teorijskim putem (konkretno, mozemo da predpostavimo da je verovatnoca pogotka 0.2 i da treba osvojiti 3 poena za pobedu).

Da li neko ima ideju kako bi to moglo da se uradi?

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 19:25 - pre 162 meseci}

Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk

H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena

p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8711
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 20:51 - pre 162 meseci}

Citat:

kandorus: Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk

H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena

p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1

Hihihi! Probaj da rešiš tako kako si napisao za neki konkretan slučaj, recimo p=2/3, k=2.

@beyn

Neka je

verovatnoća da će igrač pobediti ako trenutno ima

bodova.

,

,

za

.

Kada rešiš ovaj sistem jednačina,

je vrednost koja te zanima.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

beyn
Branko Popovic
Student
Beograd

Član broj: 261796
Poruke: 4
*.dynamic.isp.telekom.rs.

+2 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 21:38 - pre 162 meseci}

@Nedeljko

Hvala na odgovoru.
Samo jos jedno pitanje. Da li postoji neka teorema na kojoj se bazira to sto si naveo (ako postoji samo navedi ime zato sto cu je lako naci) tj. iz cega si to dobio ili si do resenja dosao cistom logikom ?

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.41.*

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 22:25 - pre 162 meseci}

Da ne treba slucajno

? Ako je p verovatnoca da pogodi?

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 23:12 - pre 162 meseci}

@Hihihi!

U čemu je problem? Ja sam samo izračunao verovatnoću da strelac sakupi k poena. Slično važi i za -k poena:

p(-k) = p^k/(1-p)^k, 1/2 < p <= 1
p(-k) = 1, 0 <= p <= 1/2

Za k=2 i p=2/3 dobije se da sa verovatnoćom 1 (sigurno) strelac osvaja 2 poena ali ne tvrdim da će da pobedi.

Kad smo već kod računanja. Za k=0 i p=0.5, koliko je pk po tvojoj računici?

Odgovor na temu

beyn
Branko Popovic
Student
Beograd

Član broj: 261796
Poruke: 4
*.dynamic.isp.telekom.rs.

+2 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 23:14 - pre 162 meseci}

@Darkosos

Meni deluje logicno ono sto je Nedeljko napisao, zato sto uvek iz i-te situacije u kojoj se nalazimo (-k<i<k) mozemo da idemo napred za jedan (u stanje i+1) sa verovatnocom pogotka (ako postignemo pogodak) i nazad za jedan (u stanje i-1) sa verovatnocom promasaja.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.41.*

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{19.01.2012. u 23:20 - pre 162 meseci}

Nemam pojma, mozda, ja sam to shavtio kao dolazak u situaciju i :) ili preko i+1 sa promasajem ili preko i-1 sa pogotkom...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8711
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 02:17 - pre 162 meseci}

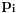
je verovatnoća da pobediš ako si trenutno u poziciji

. Treba samo čitati.

Radi se naravno o uslovnoj verovatnoći.

Pretpostavimo da je

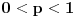
(preostali slučajevi su trivijalni). Neka je

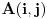
događaj da je igrač u

-tom gađanju imao

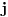
poena i

događaj da je pobedio. U tom slučaju je je

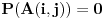
ako i samo ako je

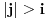
ili je

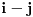
neparan broj. U suprotnom je

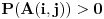
. Ovo mi treba zato što se uslovna verovatnoća može računati samo po uslovu čija je verovatnoća različita od nule.

Pretpostavimo da je

i da je

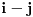
paran broj.

Ako je

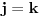
, onda je

.

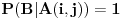
Ako je

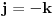
, onda je

.

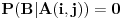
Ako je

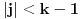
, onda je

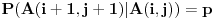
i

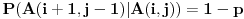
, odnosno

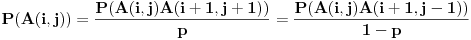
i pritom je

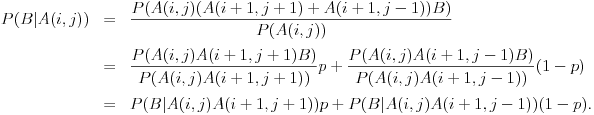
Tebi ostavljam da dokažeš da je u ovom slučaju

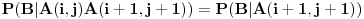
. Skup elementarnih ishoda je skup konačnih nizova nula i jedinica (pogotci i promašaji) takav da... Razmotri događaje

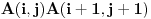
i

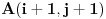
, tj. odnos skupova početaka nizova do pozicije

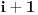
i završnih delova nizova, odgovarajuće verovatnoće itd. Na kraju vidi šta se krati i to je to.

U dobijenom sistemu jednačina

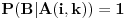
kada je

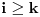
i

iste parnost kao

,

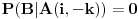
kada je

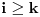
i

iste parnost kao

,

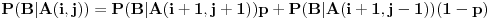
kada je

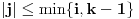
i

iste parnost kao

,

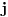
možeš ignorisati

, a ti vidi zašto (imaš beskonačno mnogo nezavisnih sistema sa istim rešenjem).

_{[Ovu poruku je menjao Nedeljko dana 20.01.2012. u 15:40 GMT+1]}

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 02:55 - pre 162 meseci}

U ovom zadatku ne važi da je

Citat:

Skup elementarnih ishoda je skup konačnih nizova nula i jedinica (pogotci i promašaji)

već važi:

jer je slučajna veličina vezana za vrednost poena (+1 ili -1).

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.41.*

+64 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 10:44 - pre 162 meseci}

Ja se izvinjavam, ovo je postalo previse komplikovano za mene :)

Odgovor na temu

beyn
Branko Popovic
Student
Beograd

Član broj: 261796
Poruke: 4
*.dynamic.isp.telekom.rs.

+2 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 11:26 - pre 162 meseci}

Veliko hvala Nedeljko. Stvar je sada razjasnjena.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 12:50 - pre 162 meseci}

Pa lepo, da li bi hteo i nama da razjasniš? Baš smo radoznali.

Meni je ovo Nedeljkovo "rešenje" zanimljivo i zato jer (množi i) deli dogadjaje i verovatnoće. Na primer jedan od članova u tim sabircima je

Neki bi rekli "deli babe i žabe". E sad to je moguće jer je tada rezultat oblika "a baba po b žaba". Problem je što se u Nedeljkovom rezultatu dobije verovatnoća. Obaška što A(r) nije definisano. Ali dobro šta se ja razumem.

_{[Ovu poruku je menjao kandorus dana 20.01.2012. u 14:46 GMT+1]}

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8711
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 14:47 - pre 162 meseci}

Ispravljene su uočene greške u kucanju. No, rešenje je očigledno i ranije bilo jasno onome kome vredi objašnjavati, a zaista ne mogu da objašnjavam onima koji mogu da napišu ovako nešto

Citat:

kandorus: Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk

H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena

p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1

ili

Citat:

kandorus: @Hihihi!

U čemu je problem? Ja sam samo izračunao verovatnoću da strelac sakupi k poena. Slično važi i za -k poena:

p(-k) = p^k/(1-p)^k, 1/2 < p <= 1
p(-k) = 1, 0 <= p <= 1/2

Za k=2 i p=2/3 dobije se da sa verovatnoćom 1 (sigurno) strelac osvaja 2 poena ali ne tvrdim da će da pobedi.

Kad smo već kod računanja. Za k=0 i p=0.5, koliko je pk po tvojoj računici?

ili

Citat:

kandorus: U ovom zadatku ne važi da je

Citat:

Skup elementarnih ishoda je skup konačnih nizova nula i jedinica (pogotci i promašaji)

već važi:

jer je slučajna veličina vezana za vrednost poena (+1 ili -1).

Ako darkosos bude tražio konkretnija pojašnjenja, potrudiću se, a oko tebe kandorus jednostavno nema svrhe truditi se.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{20.01.2012. u 16:36 - pre 162 meseci}

Slučajna promenljiva iz postavke zadatka nije indikator dogadjaja (a što je ti predstavljaš navodeći da su u pitanju nizovi nula i jedinica). Ovde slučajna promenljiva uzima vrednost iz skupa {-1, 1}. Za indikator dogadjaja važi E(I) = p. Medjutim za slučajnu promenljivu koja uzima vrednost iz skupa {-1, 1} sa verovatnoćom {1-p, p} važi

E(X) = -1(1-p) + 1p = 2p - 1

Jasno je da te dve slučajne veličine nemaju istu raspodelu. Kako možeš dobiti tačno rešenje ako ti verovatnosni model nije korektan?

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{21.01.2012. u 12:21 - pre 162 meseci}

Ovo što je Nedeljko izračunao u poslednjoj formuli se svodi na isto ono što sam ja dao za B1. Medjutim, kao što sam već napomenuo, primena te formula ne daje konačan odgovor na zadatak jer ne uzima u obzir mogućnost sakupljanja -k poena kada je partija izgubljena.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8711
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{21.01.2012. u 14:44 - pre 162 meseci}

kandorusu nemam nameru da odgovaram. Ovde pišem samo zbog onih koje bi on mogao da dovede u zabunu. Ako rešenje nije jasno onome kome treba da bude jasno, molim da mi to napiše, da se ne bih raspravljao sa kandorusom.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{21.01.2012. u 15:29 - pre 162 meseci}

Ne radi se niokom ponaosob već o rešenju. Ti osporavaš ono što sam napisao a sam dolaziš do iste formule. Medjutim ta formula nije potpun odgovor na zadatak. Osim toga ostaje otvoreno pitanje tipa promenljive. Ti polaziš od pretpostavke da je reč o promenljivoj tipa indikator dogadjaja. Ali takva pretpostavka nikako ne stoji. Bar je to očigledno jer indikator dogadjana ne može da ima negativnu vrednost a slučajna promenljiva iz ovog zadatka može. Matematičko očekivanje nije isto, disperzija (4p(1-p)) nije ista, ma to nisu promenljive sa istom raspodelom.

A osim toga, upravo zahvaljujući mojim primedbama ispravio si neke greške u tvom rešenju.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.yourproxyhost.com.

+443 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{22.01.2012. u 01:43 - pre 162 meseci}

Po uslovu zadatka je

P(-k) = 0, P(k) = 1

Prelazak iz stanja sa (-k+2) pogodaka u stanje sa (-k+1) pogodataka ostvaruje se sa verovatnoćom (1-p) pa je

P(-k+1) = P(-k+2)(1-p)

Ako je stanje sa (k-1) pogodaka tada sledećim hicem pobedjuje sa verovatnoćom p ili se prelazi u stanje (k-2) sa verovatnoćom (1-p). Zato je

P(k-1) = p + (1-p)P(k-2)

Za -k+1 < j < k-1 važi

P(j) = pP(j+1) + (1-p)P(j-1)

(p + (1-p))P(j) = pP(j+1) + (1-p)P(j-1)
pP(j) + (1-p)P(j) = pP(j+1) + (1-p)P(j-1)
p( P(j) - P(j+1) ) = (1-p)( P(j-1) - P(j) )

P(j) - P(j+1) = ( P(j-1) - P(j) )(1-p)/p

Ako se označi r = (1-p)/p dobije se

P(-k+2) = P(-k+1)(1+r)
P(-k+3) = P(-k+1)(1+r+r²)
...
P(j) = P(-k+1)(1+r+r² + ... + r^j+k-1) (*)

P(j) = P(-k+1)(1 - r^j+k)/(1 - r) (**)

r mora biti različit od 1 (u suprotnom je p=1/2).
Za j = k dobije se:

P(k) = P(-k+1)(1 - r^2k)/(1 - r)

1 = P(k) = P(-k+1)(1 - r^2k)/(1 - r)

P(-k+1) = (1 - r)/(1 - r^2k)

Koristeći dobijeni izraz za P(-k+1) i na osnovu (**) verovatnoća pobede je:

(*) Ako je p = 1/2 tada 1+r+r² + ... + r^j+k-1 = j+k, pa je P(-k+1) = 1 / 2k
P(0) = k/2k = 1/2

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8711
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Problem oko teorijskog racunanja verovatnoce

^{22.01.2012. u 03:16 - pre 162 meseci}

Ovaj put ti je rešenje dobro jer si prepisao uslove iz moje prve poruke i njih rešio.

Citat:

,

,

za

.

Citat:

kandorus: P(-k) = 0, P(k) = 1
P(j) = pP(j+1) + (1-p)P(j-1)

No, uporedi ovo sa svojom prvom porukom

Citat:

kandorus: Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk

H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena

p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

[es] :: Matematika :: Problem oko teorijskog racunanja verovatnoce

Strane: 1 2

[ Pregleda: 5907 | Odgovora: 38 ] > FB > Twit

Srodne teme

25.01.2009. Supremum funkcije
07.02.2009. Treba mi pomoć oko verovatnoće
17.05.2010. proracun vratila-problem ili ne
13.03.2009. Pomoc oko verovatnoce.....
02.05.2009. Zaokruzivanje prilikom racunanja - POMOC
26.03.2010. Problem oko racunanja prosjeka
17.09.2010. MATLAB kumulativna funkcija verovatnoce
27.02.2011. Paralelno racunanje pomocu HLSL - Problemi
30.06.2011. Praktican problem iz verovatnoce.

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.