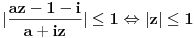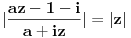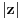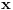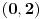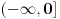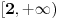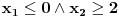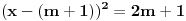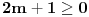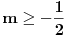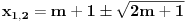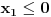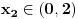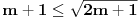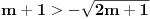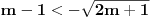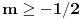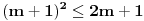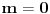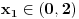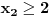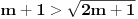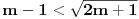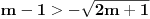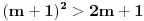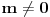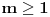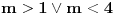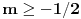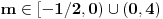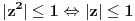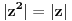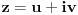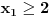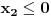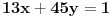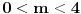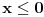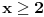Nekoliko interesantnih zadataka.Prvi zadatak.Predstavi broj
kao linearnu kombinaciju brojeva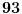 
i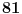 
,
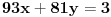,pokusao sam da resim ovo gledajuci neku od prethodtema gde je bil reci oko Euklidovog algoritma i vido sam onaj uslov da je 
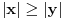,ali ja dobijam skroz suprotno nikako mi ne uspeva.Drugi zadatak:Dokazati da od jednacina
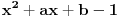i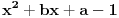 
bar jedna ima realna resenja.Ja sam ovako poceo ,odredim diskriminatnu za prvu jednacinu 
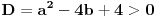,za drugu 
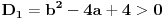,i sad kako da na osnovu ovoga zakljucim koja jednacina ima realna resenja.Treci zadatak:Za koje vrednosti realnog parametra
, je tacno jedan koren jednacine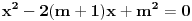 
u intervalu 
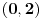.E sad ovde mislim da isto zbog ovoga intervala treba da je Diskiriminana veca od nule al nikako mi nije jasno i buni me zbog ovoga tacno jedan koren jednacine.Cetvrti zadatak:Ustvari jedno pitanje ,radi se o sistemima ostataka,Za ostatke po mogulu sedam imamo sledecu tabelu:
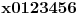
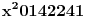meni nikako nije jasno kako su dobijeni ovi brojevi dole u vrsti x na kvadrat.P.S. ovu tabelu nisam znao da napisem izmedju svaka dva broja ima razmak ,i svakom broju ispod odgovara tacno jedan broj,razumece oni koji su radili.
Peti zadatak:Dokazati ako je
,
,
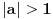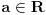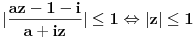.U pitanju su kompleksno brojevi al ovaj zadatka neumem ni da pocnem.
