Ako je
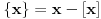
, onda važi:
Skup tačaka nagomilavanja niza
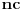
je jednak
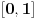
akko je c iracionalan broj.
Neka je
,
,
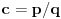
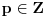
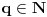
. Tada je
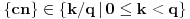
, pa pošto je taj skup konačan, skup tačaka nagomilavanja ne može biti
.
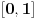
Neka je
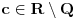
. Tada je
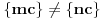
za
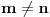
. Zaista, ako je
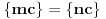
za
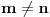
, onda je
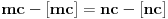
, pa je
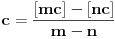
suprotno iracionalnosti broja
. Jasno je da zbog
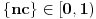
ovaj niz ima bar jednu tačku nagomilavanja
.
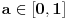
Neka je
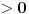
. Tada mogu naći različite
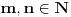
takve da je
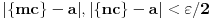
, pa je
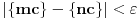
. Određenosti radi, možemo pretpostaviti da je
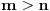
. Zbog
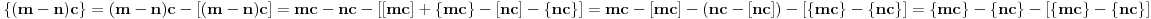
za
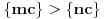
važi
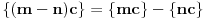
a u suprotnom
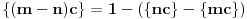
. Stoga je bar jedna od tačaka
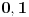
tačka nagomilavanja niza
.
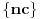
Ako je jedinica tačka nagomilavanja, onda se za bilo koje
može naći
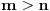
takvo da je
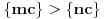
. No, onda je
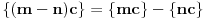
, pa je i nula tačka nagomilavanja. Dakle, nula je tačka nagomilavanja u svakom slučaju.
Drugi način da se dokaže da je nula tačka nagomilavanja je sledeći:
Neka je
proizvoljno i neka je
najmanji prirodan broj za koji je
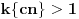
. Takav broj postoji (i veći je od 1) zato što je
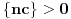
budući da je broj
iracionalan. Obzirom da je
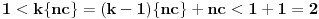
, važi
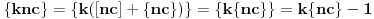
. Ako bi bilo
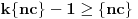
, onda bi bilo
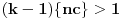
suprotno izboru broja
. Dakle,
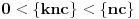
. Neka je
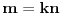
ako je
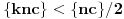
, odnosno
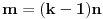
u suprotnom. Tada je
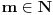
takav da je
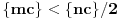
, pa je nula zaista tačka nagomilavanja.
Dokažimo sada samo tvrđenje.
Neka je sada
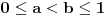
i
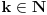
takvo da je
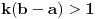
. Izaberimo takvo
da važi
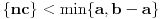
i neka je
najmanji prirodan broj za koji je
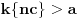
. Tada mora biti
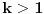
i
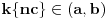
. Zaista, u suprotnom bi bilo
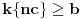
, odakle bi sledilo da je
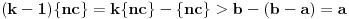
suprotno izboru broja
. No, tada za
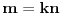
važi
.
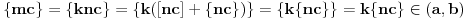
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
BESKONACNI RED-trigonometrijske f-je HITNO!
