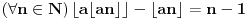Pošto izgleda ni ovo ne bi zanimalo nikoga sem Bojana, okačiću svoje rešenje:
Očigledno je
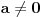
. Stavimo
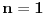
. Tada je
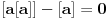
. Odatle sledi da
ne može biti negativno, pošto bi
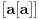
bilo nenegativno (jer bi
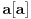
bilo pozitivno), a
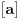
bi bilo negativno, te bi leva strana bila pozitivna. Stoga možemo nastaviti ovako:
(a)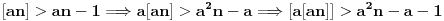 
i
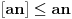
daju
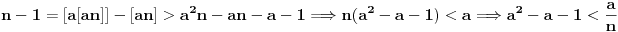(b) 
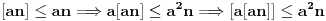
i
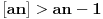
daju
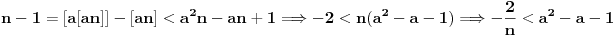
Iz (a) i (b) dobijamo
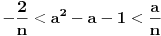
, ali pošto to mora važiti za proizvoljno veliko
, zaključujemo da je
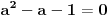
, te uz
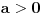
dobijamo
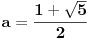
Sada moramo dokazati da identitet važi za
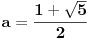
. Ako stavimo
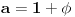
, izraz će se uprostiti u
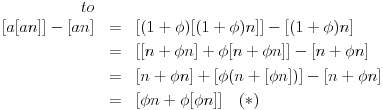
(Napomena: Ne shvatam ovo "to" koje se pojavljuje u gornjem izrazu. Je li to neki bag u LaTeX-u?)
Iz
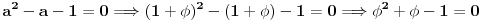
dobijamo
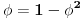
. Ako to uvrstimo u
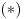
, dobijamo
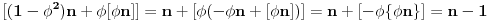
, pošto je
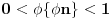
(strogost leve strane poslednje nejednakosti potiče od iracionalnosti broja
, tj. iz činjenice da navedeni razlomljeni deo nije nula ni za jedno prirodno
).
Prema tome, zaključujemo da je tražena jedinstvena vrednost parametra
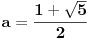[Ovu poruku je menjao Farenhajt dana 20.04.2009. u 20:30 GMT+1]
Lep problem s celim delovima
