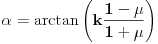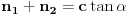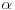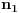Izgleda da moja metoda ala Fatina iz onog vica sa unproforcima - "dva po dva, pa se nakupilo" ne paše, pa ću kanda morati da krenem putem one koja obećava, tj. Filipove. Uzgred, taman sam mislio da pošaljem donaciju za onog miša, kad mi na pamet pade da i oni zubi na češlju imaju dužinu (ko bi rekao?), i da ceo izum svakako ima smisla. Stoga, donacija će ići za patentnu prijavu (za početak se u te svrhe odričem onog honorara što sam uspeo da "zaradim" na "veeelikoj sumi").
Dakle, ako nisam pogrešio u računici, ima tu nekoliko slučajeva koje treba razmotriti. Prethodno samo da napomenem da sam zupce sa obe strane označio sa brojevima od jedan do sedam redom, gde je prvi onaj koji je najbliži sredini terazija.
Prvi slučaj je kada su lakši dukati sa iste strane terazija, gde se dobije formula oblika:
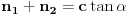
gde je c konstanta koja zavisi od dužine terazija i dužine zubaca,
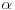
ugao otklona, a
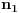
i
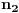
brojevi zubaca na kojima su zakačeni lakši dukati .
Drugi slučaj je kada su lakši dukati sa različitih strana terazija, a tada je formula nešto drugačija:
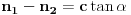
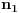
i
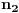
su oznake odgovarajućih zubaca, s tim da je
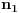
na strani koja je "izdignuta" (ova formula neće biti mnogo zanimljiva u daljem postupku, ali neka stoji).
Jedno merenje sa običnim terazijama nam je dovoljno da odredimo da li su lakši dukati sa iste strane terazija (sedam na jednu stranu, sedam na drugu).
U slučaju da su sa iste strane, te dve gomile okačimo na one zupce na već opisani način (nekoliko poruka iznad) i "očitamo"

. Pošto u najgorem slučaju imamo tri para između kojih se dvoumimo (zadatak sa proizvodom i sumom...), moramo iz trećeg merenja da odagnamo sumnju, što je trivijalno (svodi se da iz jednog merenja od tri dukata otkrijemo koji je lakši).
Kada su sa različitih strana, imamo dve gomile sa sedam dukata i u svakoj po jedan lakši. Dovoljno je da možemo pomoću pomenute naprave da u jednom merenju odredimo lakši dukat. To činimo tako što jedan izdvojimo sa strane, a ostalih šest okačimo na obe strane na zupce jedan, dva i tri. U slušaju ravnoteže u horizontalnom položaju, izdvojeni dukat je taj; ako je lakši dukat jedan od okačenih, primenjujemo nešto drugačiju formulu (sada samo jedan lakši dukat):

(oznake analogno), pa direktno očitavamo položaj lakšeg dukata.
Mislim da je ovo dovoljno, i pritom se izvinjavam na eventualnim greškama i nejasnoćama.




 Vaganje 14 dukata
Vaganje 14 dukata