Naravno. Relacije neodređenosti ne mogu da prestanu da važe u nekim slučajevima. One uvek stoje. Ako ti treba primer, uzmi talasne funkcije LHO-a za neko konkretno n, na primer za n=1 ili n=2. Račun je dosta jednostavan. Izračunaj očekivane vrednosti koordinate, impulsa i njihovih kvadrata, nađi, neodređenosti (devijacije) pa potom gustinu struje verovatnoće i gustinu verovatnoće. Videćeš da će se sve složiti.
Mislim Milane da u ovom tvom poslednjem postu ima i malo greskica!
Ono sto bi moglo da se namece kao neki zakljucak je da uvek kad imam diskretan spektar gustinu struje verovatnoce mogu da racunam kao . U slucaju kontinualnog spektra ovo ne vazi!
Neznam odakle ti takav zakljucak,moras to detaljnije da obrazlozis. Evo za slucaj slobodne cestice kod koje je potencijal V=0. Odnosno slobodna cestica ima kontinualni spektar. ;
Kao prvo sta ti je ? Zar ne treba u ovom integralu da stoji ?
Drugo ti kazes ovaj integral je , a izvod po vremenu od konstante je . Na osnovu cega ti tvrdis da je taj integral ? Prica o normiranju nam je posledica toga sto ovaj integral ne zavisi od vremena.
V je brzina cestice ako mislis na zadnji izraz za gustinu struje verovatnoce.
Moze da stoji. To je pitanje sintakse.
Uslov normiranja mora da vazi iz proste logike statisticke verovatnoce.
A to je da cestica mora da bude lokalizovana negde unutar celokupnog
konfiguracionog prostora.
[Ovu poruku je menjao Milan Milosevic dana 08.03.2008. u 14:39 GMT+1]
Neznam sto komplikujes stvari ali ajde.
Odakle je bas integral jednak jedan?
Ovako kao sto vec znas kvantna mehanika barata i predvida statistickom
verovatnocom.
Zbog cega je to tako mnogi su razlozi. Najvazniji su sto za razliku od klasicne
mehanike gde je stanje sistema u potpunosti odredeno poznavanjem dinamickih varijabli
koje mozemo istovremeno da merimo sa proizvoljnom tacnoscu. U okviru kvantne mehanike
situacija je dijametralno suprotna. Ovde postupak merenja igra bitnu ulogu.
Interesantno je videti kako mi u samom experimentu odredujemo polozaj cestice?
Prosto, bombardovanjem drugim cesticama ili fotonima efekti su slicni.
Odnosno dolazi do trajnog narusavanja stanja sistema.
To se moze najlakse uporediti sa situacijom u kojoj slepac odreduje udaljenost druge
osobe gadajuci ga lopticama od papira kao u slucaju klasicne fizile ili
kuglom za kuglanje (kvantno mehanicki salucaj) . Ako bi te neko pogodio kuglom od
5 Kg sigorno bi se tvolje stanje svesti promenilo.
Kao rezultat tih merenja mi prosto proucavamo uglove rasejanja. Odnosno
broj rasejanih cestica n za neki ugao od ukupnog broja cestica N u snopu.
Taj odnos n/N je u stavari statisticka verovatnoca.
Verovtnoca moze da uzima vrednosti u intervalu od [0,1]
gde 0 znaci da dogadaj nije moguc, a vrednost 1 potpuno siguran dogadaj.
Ovde smo dosli do toga odakle nam se u izrazu za normiranje javlja jedinica.
Kvadrat amplitude talasne funkcije daje gustinu verovatnocu nalazenja cestice u tacku prostora
odredenu vektorom polozaja u posmatranom trenutku t.
Mnozenjem sa elementom zapremine dr daje verovatnocu nalazenja cestice u nutar posmatrane
infinitenzimalne zapremine.
Ako sad prointegralimo po celokupnom prostoru uzimajuci za granice integracije beskonacnost
iako svermir nije beskonacan mi na taj nacin zakljucujemo da je verovatnoca nalazenja posmatrane
cestice u nasem kosmosu jedan. Odnosno da ce se sigurno naci unutar granice svemira.
Ako ti odavde nije jasno zasto je integral jednak jedinici ja nemogu da ti pomognem.
Ti imas tu pricu o verovatnoci samo zato sto taj integral ne zavisi od vremena! A nije tacno da taj integral ne zavisi od vremena zato sto imas tu pricu. To je ono sto ja pokusavam da ti kazem!
Potrazi u bilo kom udzbeniku kvantne mehanike zakon odrzanje verovatnoce i svuda ces naci taj izraz.
Ja ne izmisljam stvari nego ti obrazlazem onako kako je to dato u knjigama kvantne mehanike.
Ako svi grese boze moj, zasto onda da negresim i ja.
Uslov normiranja talasne funkcije na jedinicu je jedan od osnovnih zakona kvantne mehanike
koji ima veliku primenu u mnogim teoremama.
Ako mislis da to nije tacno onda to treba da dokazes
bilo matematickim dokazom bilo experimentom.
[Ovu poruku je menjao Milan Milosevic dana 09.03.2008. u 07:35 GMT+1]
Milan Milosevic: Uslov normiranja talasne funkcije na jedinicu je jedan od osnovnih zakona kvantne mehanike
koji ima veliku primenu u mnogim teoremama.
[Ovu poruku je menjao Milan Milosevic dana 09.03.2008. u 07:35 GMT+1]
Uslov normiranja talasne fje sledi iz Bornove interpretacije. A Bornova interpretacija ima smisla samo zato sto dati integral ne zavisi od vremena!
Da je fja stanja element Hilbertovog prostora je jedan od postulata KM. Kada pokazes da ti dati integral ne zavisi od vremena. A to sam ja pokazao
Gram–Schmidt-ov postupak je postupak ortogonalizacije bazisa.
I nema nikakve veze sa normiranjem talasne funkcije.
Ondosno ako ima pokazi nam kako ja ne znam.
A voleo bi nesto novo i da naucim.
petarm: Mislim da onda nemamo iste udzbenike :)! Navedi mi jedan od tih udzbenika i na kojoj strani da pogledam!
Za pocetak ne vidim da si odgovorio na ovo pitanje!
Citat:
Milan Milosevic: Gram–Schmidt-ov postupak je postupak ortogonalizacije bazisa.
I nema nikakve veze sa normiranjem talasne funkcije.
Ondosno ako ima pokazi nam kako ja ne znam.
A voleo bi nesto novo i da naucim.
Izvini kako ti konstruises Ermitove, Lezandrove, Lagerove polinome? Pa Gram Smitovim postupkom. Fja stanja koja se dobija kao resenje LHO-a je .Tzv. normirana Ermitova funkcija. Ono sto sam ja hteo da ti kazem je da u mozes napraviti ortonormiran bazis. I neke tvoje fje razlagati po vektorima bazisa.
[Ovu poruku je menjao petarm dana 09.03.2008. u 11:05 GMT+1]
Schmidt-ov postupak ortogonalizacije je postupak da se neka ne ortonormirana baza prevede u ortonormiranu i nista
vise.A razvoj proizvoljnog vektora po kompletnom ortonormiranom setu nije sam po sebi Gram–Schmidt-ov postupak.
Cak za primenu Gram–Schmidt-ov postupka neophodno je da dati vektori stanja budu normirani na jedinicu.
Sto se tice tvrdnje
Citat:
petarm: Ono sto sam ja hteo da ti kazem je da u mozes napraviti ortonormiran bazis. I neke tvoje fje razlagati po vektorima bazisa.
Sto se tice tvoje tvdnje da ne mora da vazi zakon odrzanja verovatnoce odnosno
da integral nije vremenski nezavistan ima smisla jedino ako predpostavimo da
je cestica elektron naisao na svoju anti cesticu pozitron i da se anihilirao.
Ili ako mislis da mozda postoji prelaz iz univerzuma u univerzum te da otud moze da dode do
narusavanja verovatnoce postojanosti elektrona u nasem razmatranom svetu.
Jer toje pretpostavke samo tako mogu da imaju nekog razumnog smisla
Da si pazljivo citao sta sam napisao ne bi poslao ovu poruku. Ja ne tvrdim da taj integral zavisi od vremena. Ja sam pokazao da on ne zavisi od vremena!
. I zbog toga sto je ermitski ovo je .
Ja kazem sledece da bez ovog gore ti ne mozes da znas da on ne zavisi od vremena! A sad kad si to saznao dalje mozes da nastavis svoju pricu
Kolega Milošević je napravio mali propust kod sledećeg. Napisao je
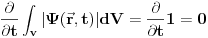
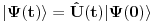
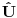
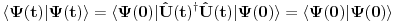
Ono što je propustio da kaže je da je , gde je evolucioni operator koji je unitaran, tako da, ako je početno stanje normirano tada je i . Dakle, kako vremenska evolucija čuva normu, uvek možemo reći da je prethodni integral konstantan, pa je prema tome njegov vremenski izvod 0.
Registrovani: 1 ( RebekaA )
Re: Kvantno mehanicka jednacina kontinuiteta
! Navedi mi jedan od tih udzbenika i na kojoj strani da pogledam! 
