Mislim da je intuitivno prilično jasno. Poprilično direktna posledica relacija neodređenosti. Impuls čestice može uzimati sve vrednosti između
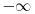
do
sa podjednakom verovatnoćom. U takvoj situaciji je nemoguće očekivati neku određenu vrednost struje, te stoga i izraz divergira. Kada kažem da izraz divergira, ne želim da kažem da je beskonačan, već da prosto nema određenu vrednost (poput
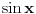
kada
).
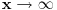
Kakvom bi to eksperimentu odgovaralo? Kada smo izmerili da je čestica u stanju
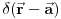
mi smo to uradili tako što smo izveli eksperiment kojim smo maksimalno lokalizovali česticu (iako je to praktično nemoguće), a kao što znamo još iz srednje škole, izvođenje takvog eksperimenta nas sprečava da izmerimo bilo šta što je povezano sa impulsom, što je u ovom slučaju struja, koja je za impuls vezana relacijom
.
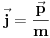
Skroz je druga stvar ako uzmemo stanje
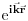
. Eksperiment kojim smo ustanovili da je čestica u ovom stanju je koncipiran tako da maksimalno precizno odredi njen impuls što automatski isključuje bilo kakvo merenje bilo čega povezanog sa položajem. Kao posledicu ćemo imati lepo definisanu struju
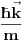
, ali ćemo imati problema sa verovatnoćom nalaženja čestice u prostoru (problem ravnih talasa o kome smo jedanput već pričali).
Dakle, relacije neodređenosti na delu.
Kvantno mehanicka jednacina kontinuiteta
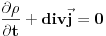
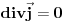
moze meriti, a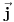 
ne. Zasto?
Registrovani: 9 ( djoka_l, zoksy, Nedeljko, valjan, Turmen, RebekaA, iculibrk, Andra_Ivic, Ultrena )
