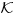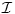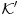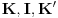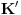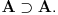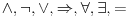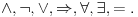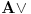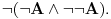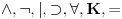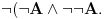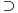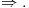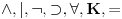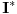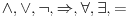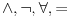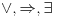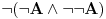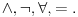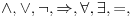OK, pogrešio sam u prethodnoj poruci. Da se popravim.
Sistem K' jeste tačno klasična logika na jeziku
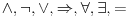
. Ne vidim u tome nikakav problem. Zbog čega ne bi bila?
Sistem K takođe jeste tačno klasična na istom jeziku. K i K' su izomorfni. Imaju izomorfne jezike.
Sistem I jeste intuicionistička logika na izomorfnom jeziku.
Možemo reći da su jezici isti. Recimo da je taj jezik
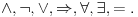
To upravo znači i da je skup formula isti.
Vratimo se sada na tvoje pitanje
Citat:
uranium: onda je lako videti da je svaka teorema intuicionističke logike, teorema i klasične logike, kao i obrnuto, svaka teorema klasične logike je teorema intuicionističke logike (zbog izomorfnosti

i
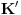
).
I šta je to sad? :)
Kada potapaš sistem K' u sistem I, ti nećeš svaki polazni logički simbol domena slikati u sebe, već u veznik koji je definljiv u logici koja je kodomen. Time se neće svaka formula domena preslikati u sebe. Recimo, formula
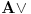
slikaće se u formulu
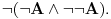
To jeste potapanje, jer se svaak teorema doemna slika u teoremu kodomena. Kada potapaš sistem I u sistem K, ti svaki polazni simbol slikaš u sebe samog, pa se samim tim i svaka formula domena slika u samu sebe. I to je potapanje, jer se svaka teorema domena slika u teoremu kodomena. Sistemi K i K' će biti u potpunosti isti, ali će sistem I imati uži skup teorema (Nemoj ovde da brzaš, pročitaj tekst do kraja, Vreba jedna "optička varka".). Dakle, neće klasična i intuicionistička logika biti iste.
Seti se samo da se svaki od intervala [0,1), (0,1] može utopiti u onaj drugi, ali da oni nikako nisu izomorfni. Ne kažem da si tvrdio suprotno, niti da to ne znaš, već samo napominjem da to treba stalno imati u vidu.
Međutim, isti simbol će u različitim sistemima označavati različite veznike. Zato je bolje da kažemo da sistem I ima jezik
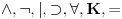
da ne bi bilo opasnosti od "optičke varke" da je u sistemu I formula
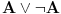
formulacija zakona isključenja trećeg. sistem K se tada utapa u sistem I, mi ćemo u principu polazne simbole iz domena slikati u izvedene simbole kodomena, pa će se formula
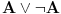
slikati u formulu
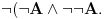
Sa druge strane, pri potapanju sistema I u sistem K ćemo polazne simbole domena slikati u polazne simbole kodomena. Na primer,
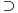
u
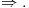
Kada se eliminiše "optička varka", onda više skup teorema sistema I nije inkluzijski uporediv sa skupom teorema sistema K. No, i ovde imamo jednu "optičku varku". Nismo uračunali simbole koji mogu biti definisani preko polaznih.
Pretpostavimo da je K'' sistem dobijen proširivanjem sistema K novim sibolima definisanim preko polaznih. Ukoliko upotrebimo barem jedan intuicionistički simbol u tom proširenju, onda zahtevamo da sistem K'' i sistem I na preseku njihovih skupova formula imaju isti skup teorema. Drugim rečima, ne dopuštamo upotrebu istog simbola u različitim značenjima. Tada možeš formirati sistem I' proširivanjem sistema I svim sibolima sistema K'' koji nisu simboli sistema I, definisanim preko polaznih simbola sistema I, tako da skup teorema sistema I' i K'' na skupu formula sistema K'' bude isti, i da skup teorema sistema K'' bude pravi podskup skupa teorema sistema I'. U obrnutom smeru se to ne može uraditi. To je zato što se svi klasični simboli mogu definisati unutar intuicionističke logike, ali se svi intuicionistički ne mogu definisati u okviru klasične logike.
Kada definišemo u sistemu I nove simbole preko polaznih, dobićemo sistem čiji je skup teorema pravi nadskup skupa teorema
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
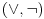 se ne razlikuje od para veznika
se ne razlikuje od para veznika 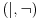 u nadračunu, ali se razlikuje u podračunu upravo zato što
u nadračunu, ali se razlikuje u podračunu upravo zato što 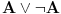 jeste teorema, a
jeste teorema, a 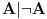 nije teorema. To možeš uporediti sa teorijom pramenova euklidske i apsolutne geometrije. Za paraboličke i hiperboličke pramenove važe iste teoreme u euklidskoj geometriji, ali ne važe iste teoreme u apsoltnoj geometriji. Šta je tu sporno ili neobično?
nije teorema. To možeš uporediti sa teorijom pramenova euklidske i apsolutne geometrije. Za paraboličke i hiperboličke pramenove važe iste teoreme u euklidskoj geometriji, ali ne važe iste teoreme u apsoltnoj geometriji. Šta je tu sporno ili neobično?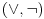 i
i 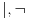 jesu isti (i sintaksno i semantički) u nadračunu, odnosno različiti u podračunu. Razne formule koje su ekvivalentne u ZFC, ne moraju biti ekvialentne u ZF, pa se pri izbacivanju aksiome izbora mnogi pojmovi cepaju na više podpojmova. Sve je to krajnje uobičajeno u matematici. Uopšte ne razumem poentu tvoje priče.
jesu isti (i sintaksno i semantički) u nadračunu, odnosno različiti u podračunu. Razne formule koje su ekvivalentne u ZFC, ne moraju biti ekvialentne u ZF, pa se pri izbacivanju aksiome izbora mnogi pojmovi cepaju na više podpojmova. Sve je to krajnje uobičajeno u matematici. Uopšte ne razumem poentu tvoje priče.



 Re: Logika, filozofija
Re: Logika, filozofija