Filmilov račun nije dobar jer ne postoji događaj tipa "novčić je fer", odnosno "novčić je nefer". Događaj je uvek neki skup elementarnih ishoda. Ovde su ishodi tipa paldalo je "PPPGPGGPGGG...PGP u tom redosledu". Pretpostavka da je novčić fer ili da nije fer se zove statistička hipoteza, pri čemu bez stavljanja cele priče u neki širi kiontekst nema smisla govoriti o njenoj verovatnoći.
Ako je H hipoteza da je novčić fer, a A suprotna hipoteza, onda se verovatnoća padanja glave pod prvom pretpostavkom obeležava sa P
H(G), dok o verovatnoći istog događaja pod pretpostavkom A nema smisla ni govoriti bez stavljanja cele priče u neki širi kontekst jer odgovarajuća slučajna promenljiva nema jednu tačno određenu raspodelu (nezavisno od toga da li je ta raspodela poznata ili nepoznata), odnosno nema jedne fiksirane funkcije verovatnoće. U svakom slučaju, tada formula P(H)+P(A) nema nikakvog smisla
U svakom slučaju, ako su bacanja nezavisna broj palih glava nakon određenog broja bacanja ima binomnu raspodelu, ali ne znamo koju jer ne znamo verovatnoću padanja glave. Tek kada fiksiramo verovatnoću p padanja glave, možemo govoriti o verovatnoći nekog ishoda.
Ako pak verovatnoća p padanja glave zavisi od nekih slučajnih veličina i ako znamo raspodelu F verovatnoća za p, onda je verovatnoća da u n bacanja broh g glava koji je pao bude jednak k jednaka
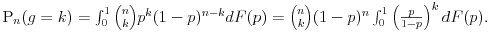
Naravno, ovde se radi o odgovarajućem Lebeg-Stiltjesovom integralu. Ukoliko je raspodela F ravnomerna, onda je dF(p)=dp, a ako je apsolutno neprekidna sa gustinom D(p), onda je dF(p)=D(p)dp. U tom slučaju je P(p=c)=0 za bilo koju vrednost c, pa nema smisla govoriti o nečemu kao što je uslovna verovatnoća P(E|p=c), gde je E neki događaj, dok će zbog P(nije p=c)=1 važiti P(E|nije p=c)=P(E).
No, ako je ovaj kontekst u pitanju, onda se zapravo za slučaj n bacanja za skup elementarnih ishoda uzima skup uređenih parova čija je prva komponenta p, a druga niz od n slova od kojih je svako G ili P, a za verovatnoću događaja da padne određeni niz S, a p pripadne merljivom skupu E vrednost
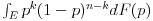
za neku funkciju raspodele F na segmentu [0,1] i k jednako broju slova G u nizu S. U svakom slučaju, nigde se ne govori o verovatnoći da raspodela bude ova ili ona, jer nema potrebe za tim. Drugim rečima, takva proširenja konteksta se nigde ne razmatraju, jer se odmah sve šta treba ubaci u algebru događaja i funkciju verovatnoće.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.