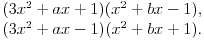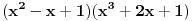Pa na ispitu se zadaci baš i ne sastavljaju da bi se pogađala rešenja. Treba znati sledeću teoremu:
Citat:
Neka polinom
ima celobrojne koeficijente. Da bi broj p/q bio koren tog polinoma, gde su p,q uzajamno prosti celi brojevi i q različito od nule, neophodno je da p|a
0 i q|a
n.
Tako nalaziš najpre sve njegove racionalne nule, pa dališ dok ne stigneš do polinoma koga znaš da faktorišeš. ponekad je potrebno otarasiti se višestrukih faktora. Oni se nalaza preko NZD(p,p'). Tvoj drugi polinom možeš da podeliš dva puta da sa x-1.
Prvi nema racionalne nule, a nad prstenom celih brojeva bi jedin e faktorizacije mogle da mu budu oblika
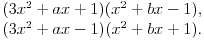
No, lako se vidi da ovaj polinom nema faktorizacije tog oblika, pa je po Gausovoj lemi nerastavljiv i nad poljem racionalnih brojeva.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Faktorizacija polinoma
