Algebarske jednačine su jednačine oblika

gde su

neke konstante koje se zovu koeficijenti te algebarske jedna;ine. Ako je pritom
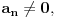
onda se još kaže i da je ta jednačina stepena
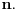
Broj je transcedentan ako nije rešenje niti jedne algebarske jednačine stepena berem jedan sa celim (ili algebarskim) koeficijentima. Jako je teško dokazati transcedentnost neke konstante. Najpoznatiji transcedentni brojevi su

i

. Otvoren je problem da li postoji polinom
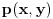
sa dve promeljive i celim koeficijentima od kojih je barem jedan različit od nule, ali tako da bude
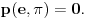
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.