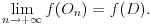Uočimo proizvoljnu tačku O poluprave p i q sa temenom O koje ne leže na jednoj pravoj. Za realan pozitivan broj x sa p
x označićemo tačku poluprave p koja je na rastojanju x od tačke O, a sa q
x tačku prave q koja je na rastojanju x od tačke O. Definišimo još funkcije P(x) i Q(x) sa P(x)=f(p
x), Q(x)=f(q
x). Sa s označimo simetralu ugla pOq. Za proizvoljne x,y>0 centar upisanog kruga S u trougao Op
xq
y se nalazi na pravoj s, pa se refleksijom u odnosu na pravu s preslikava u sebe. Ista refleksija prevodi tačku p
x u tačku q
x, kao i tačku q
y u tačku p
y. To tačno znači da trouglovi Op
xq
y i Oq
xp
y imaju zajednički centar upisanog kruga S (jer izometrija prevodi centar upisanog kruga u centar upisanog kruga) pa važi
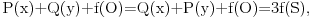
odnosno posle skraćivanja sa f(O) i sređivanja
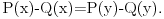
No, budući da su x i y bili proizvoljni pozitivni realni brojevi, ovo tačno znači da je funkcija P(x)-Q(x) konstantna. To upravo znači da je P(x)=Q(x)+C za neku konstantu C. Ovo znači da ako uočimo bilo koje dve poluprave sa zajedničkim temenom, funkcija f se na tim polupravama "razlikuje za konstantu" koja naravno zavisi od izabranih polupravih.
Označimo sada sa s
x, gde je x pozitivan realan broj tačku na pravoj s koja pripada konveksnom uglu sa kracima p i q i koja je na rastojanju x od tačke O. Definišimo funkciju S(x) sa S(x)=f(s
x). Pretpostavimo da je S(k) centar upisanog kruga u trougao Op
xq
x za x=1. Može se pokazati da je zapravo
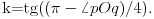
No, tada iz činjenice da sličost prevodi centar upisanog kruga u centar upisanog kruga i iz prethodnog razmatranja sledi da za svako x>0 važi formula
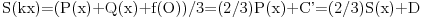
za neke konstante C' i D. Ovde je naravno korišćena činjenica da se finkcija f na polupravama p,q i s "razlikuje samo za konstantu". Mi smo to dokazali za poluprave p i q, ali pošto su one bile proizvoljne nekolinearne poluprave sa zajedničkim temenom, isto će važiti i za poluprave p,q i s.
Uočimo sada proizvoljnu polupravu a sa temenom O i poluprave b i c, takođe sa temenom O takve da poluprave a i b zaklapaju ugao (pi/2)-2 arctg(1/2), a poluprave a i c ugao (pi/2)-2 arctg(1/4). Na način kao gore zaključuje se da postoje konstante M i N takve da uz sličnu simboliku kao gore za svako x>0 važi
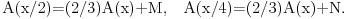
Iz prve jednakosti sledi da je i
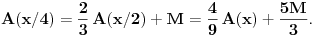
Ta jednakost zajedno sa drugom od gore navedenih jednakosti daje
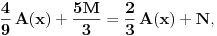
odakle najzad sledi
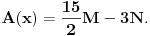
To upravo znači da je na polupravoj a funkcija f konstantna. Međutim, pošto je a bila proizvoljna poluprava sa proizvoljnim temenom O, to će značiti da je funkcija f konstantna na svakoj polupravoj, a kako se svake dve tačke nalaze na nekoj polupravoj, odatle odmah sledi da funkcija f ima istu vrednost u bilo kojim dvema tačkama, to jest da je konstantna.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Re: Popunjavanje prostora i podela ravni.
Registrovani: 5 ( enigma78, Pajica Ristic, Bojan Basic, dusanboss, valjan )
