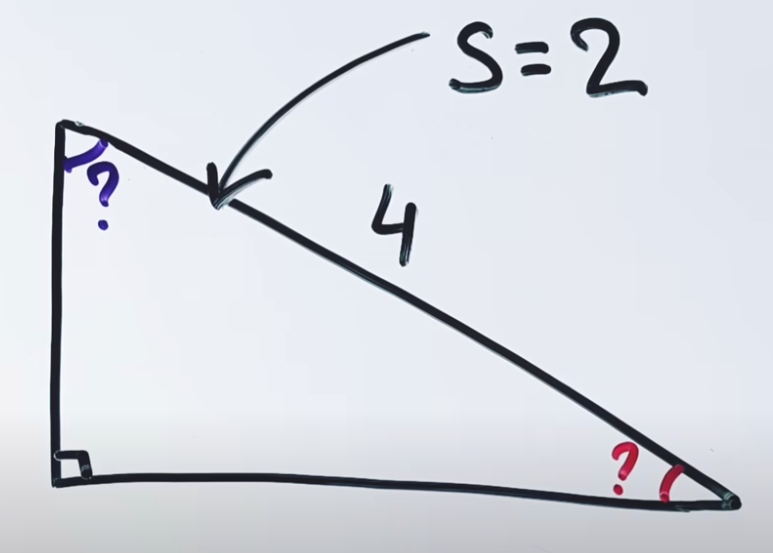
Pitanje nije kako resiti zadatak, vecina forumasa ce ti dati rezultat relativno brzo. Pitagora + kalkulator, par puta arccos() i arcsin() i dobijes uglove od 75 i 15 stepeni.
Ali secajuci se srpskog sadomazohistickog skolstva, cisto sumnjam da ce ljudi iz skupa { ucitelji(ce)*, nastavnic[ie], profesori(ce)* } priznati takvo resenje ... a velika je verovatnoca da ce reci: zabranjeni su kalkulatori na pismenom / kontorlnom / ispitu ...
Tako da se ovde verovatno trazi cinculiranje s trigonometrijom, u smislu formula za polovinu ugla, dvostruki ugao i tako to. Uglavnom, ako oznacis hipotenuzu sa
c, pocinjes od dve jednacine koje su ocigledne:
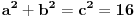
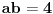
Ako je ab = 4, tada je 2ab = 8, pa hiphop kombinacijama prvu jednacinu mozes da prikazes kao kvadrat zbira ili kvadrat razlike i da od toga formiras 2 jednacine:
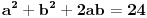
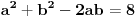
odatle dobijas:
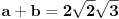
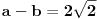
Sada ovo gore saberes i dobijas rezultat za stranice a i b:
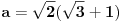
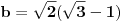
E sad, tu se verovatno dale treba cimati s onim silnim trigonomentrijskim formulama za dvostruke uglove i polovine ugla, jer je sqrt(3) kosinus ugla od 30 stepeni ... pa raznim trange-frange operacijama dodjes do rezultata.
E, mene mrzi da se dalje patim s tim ...
P. S. U eri gde AI preti da zameni gomilu poslova maltretirati decu ovakvim stvarima je besmisleno. Pogotovo je besmisleno i to ako im ne das te trigonometrijske formule da koriste za vreme ispita, vec im das samo papir i olovku, a ako ih uhvatis s puskicama obaras ih ... i tako ih pretvaras u bubalice besmislenih stvari, koje ce ionako zaboraviti cim dobiju diplomu. Nikakvo cudo sto Srbija ima najgore rezultate na PISA testovima. Zemlja bubalica!