Jedinu grešku koju sam video je zaboravljenja četvorka u prevođenju u faktorski oblik:
Piše:
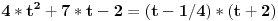
Treba:
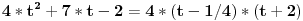
To menja krajnje rešenje, koje nisi ni napisala.
Ispravi i trebalo bi da se uklapa.
Evo ti malo urađenih primera:
http://www.puskice.org/downloa...3%20zbirka%20by%20Hijavata.pdf
Sa FON-a su zadaci.
Nije baš nešta ekstra, ali pomaže.
Ne sviđa mi se što linearnu DJ I reda rešava po formuli, a ne peške smenom y=u*v.
Jedna od boljih knjiga je od Dr Dušana Belajčića sa arhitekture.
Zove se DIFERENCIJALNE JEDNAČINE.
Mnogo dobro je objašnjeno i ima dosta urađenih primera.
[Ovu poruku je menjao miki069 dana 21.03.2014. u 00:05 GMT+1]