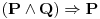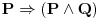a) (samo) dovoljan;
b) (samo) potreban
c) potreban i dovoljan
d) ni potreban ni dovoljan;
Ne kontam zasto bi mu bio dovoljan a znam da mu nije potreban. Nije mu potreban a dovoljan je po meni suvisan u ovoj situaciji.
Moji proizvoljni iskazi su: P>idem u skolu; Q>pada kisa;




 Logicki problem;
Logicki problem;