 realne promenljive možemo pridružiti jednu intervalnu funkciju
realne promenljive možemo pridružiti jednu intervalnu funkciju 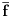 koja intervalima pridružuje intervale tako da važi:
koja intervalima pridružuje intervale tako da važi: 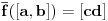 ako je interval
ako je interval 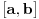 podskup domena funkcije
podskup domena funkcije  i za svako
i za svako 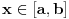 važi
važi 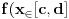 . Naravno, uvek se može staviti da je
. Naravno, uvek se može staviti da je 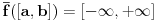 , ali od toga nema nikakve koristi. Cilj je da dobijeni interval bude po mogućstrvu što uži.
, ali od toga nema nikakve koristi. Cilj je da dobijeni interval bude po mogućstrvu što uži.Intervalna algebra omogućava da kontrolišemo, kako grešku odsecanja ili zaokrugljivanja ili računa (što je isto), tako i ukupnu grešku, koja uključuje i grešku merenja i grešku metode. Vrednost izraza izračunatog u intervalnoj algebri je interval kome garantovano pripada tačna vrednost izraza. Jedna od intervalnih biblioteka za C++ uključena je u boost. Evo primera njene primene na računanje sinusa pomoću tejlorovog razvoja.
Code:
#include <boost/numeric/interval.hpp>
using namespace boost;
using namespace numeric;
using namespace interval_lib;
typedef interval<double> real;
real sin(double arg) {
real x(arg);
const real pi2(6.283185307179586, 6.2831853071795867);
int factor = 1;
if (x == 0) {
return real(0);
}
if (x < 0) {
factor = -1;
x = -x;
}
real q = x / pi2;
q -= floor(q.upper());
if (q.upper() > 0.5) {
factor = -factor;
q -= 0.5;
}
if (q.upper() > 0.25) {
q = -q + 0.5;
}
x = q*pi2;
real x2 = -x*x;
real s(0);
real f = x;
int n = 1;
real approximation(qMin(0.0, x.lower()), qMax(0.0, x.upper()));
while (true) {
s += f;
n += 2;
f *= x2;
f /= n*(n-1);
real newApproximation = s + f;
newApproximation = real(qMin(newApproximation.lower(), s.lower()), qMax(newApproximation.upper(), s.upper()));
newApproximation = real(qMax(newApproximation.lower(), approximation.lower()), qMin(newApproximation.upper(), approximation.upper()));
if (newApproximation.lower() == approximation.lower() && newApproximation.upper() == approximation.upper()) {
break;
}
approximation = newApproximation;
}
if (factor == -1) {
return -approximation;
}
return approximation;
}
#include <boost/numeric/interval.hpp>
using namespace boost;
using namespace numeric;
using namespace interval_lib;
typedef interval<double> real;
real sin(double arg) {
real x(arg);
const real pi2(6.283185307179586, 6.2831853071795867);
int factor = 1;
if (x == 0) {
return real(0);
}
if (x < 0) {
factor = -1;
x = -x;
}
real q = x / pi2;
q -= floor(q.upper());
if (q.upper() > 0.5) {
factor = -factor;
q -= 0.5;
}
if (q.upper() > 0.25) {
q = -q + 0.5;
}
x = q*pi2;
real x2 = -x*x;
real s(0);
real f = x;
int n = 1;
real approximation(qMin(0.0, x.lower()), qMax(0.0, x.upper()));
while (true) {
s += f;
n += 2;
f *= x2;
f /= n*(n-1);
real newApproximation = s + f;
newApproximation = real(qMin(newApproximation.lower(), s.lower()), qMax(newApproximation.upper(), s.upper()));
newApproximation = real(qMax(newApproximation.lower(), approximation.lower()), qMin(newApproximation.upper(), approximation.upper()));
if (newApproximation.lower() == approximation.lower() && newApproximation.upper() == approximation.upper()) {
break;
}
approximation = newApproximation;
}
if (factor == -1) {
return -approximation;
}
return approximation;
}
Dakle, za svako
 neka je
neka je  interval kome pripadaju sve moguće vrednosti oblika
interval kome pripadaju sve moguće vrednosti oblika 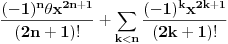 za
za 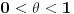 . Jasno je da za to koristimo intervalnu algebru. Mada se greška metode (ostatak) smanjuje sa povećavanjem
. Jasno je da za to koristimo intervalnu algebru. Mada se greška metode (ostatak) smanjuje sa povećavanjem  greška računa će biti sve veća i veća, pa će interval
greška računa će biti sve veća i veća, pa će interval  da se proširuje posle nekog
da se proširuje posle nekog  . Uz oznaku
. Uz oznaku 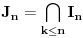 , tačna vrednost sinusa će svakako pripadati svakom od intervala
, tačna vrednost sinusa će svakako pripadati svakom od intervala 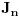 , jer pripada svakom od intervala
, jer pripada svakom od intervala  i niz intervala
i niz intervala 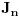 će biti neopadajući, ali će posle nekog vremena biti konstantan. Stoga izračunavanje treba prekinuti u trenutku kada
će biti neopadajući, ali će posle nekog vremena biti konstantan. Stoga izračunavanje treba prekinuti u trenutku kada 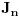 bude jednako sa
bude jednako sa 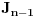 .
.Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Intervalna algebra i primena
Intervalna algebra i primena