Ne mrzi me, ali trenutno nemam vremena, pa ću pokušati da ukratko izdvojim najbitnije detalje. Algoritme ćemo zapisati u matričnim oblicima, i pozvaćemo se na činjenicu da dotični konvergiraju akko matrice uz promenljive u takvim zapisima konvergiraju, tj. ako su im sve sopstvene vrednosti po modulu manje od

. U primeru kada Gaus—Zajdelov postupak konvergira dok Jakobijev divergira za pomenute matrice imamo karakteristične jednačine
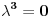
i
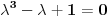
, redom, i to je sve što nam treba.
Ako nešto treba bolje da se pojasni, javi pa ću to učiniti čim budem mogao (ako ne pre vikenda, onda za vikend sigurno).
Ljubičice crvena, što si plava kô zelena trava.