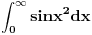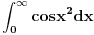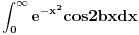Prva dva mogu. Recimo integral
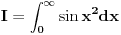
.
Kvadriramo gornji integral, vodeći pri tome računa da je integral u principu suma, tako da kao rezultat kvadriranja dobijamo dvostruku sumu
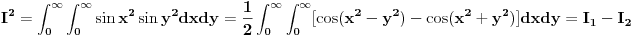
Sada treba rešiti ova dva dvostruka integrala. Prvi se rešava uvođenjem smene
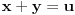
i
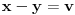
, a drugi uvođenjem polarnih koordinata. Prilikom integracije pojaviće ti se integrali oblika
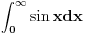
Njih rešavaš sledećim trikom. Staviš da je
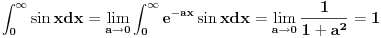
Slično i za integrale sa kosinusom. Eto, naučio si nekoliko novih trikova, a sada malo vežbaj ;)
Za treći ne znam sigurno, ali mislim da ne može.