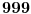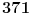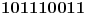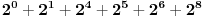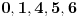Citat:
cassey: Npr. ako bi svaki mis popio iz jedna flase, on bi sigurno mogao izneti njih
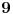
.
Da ovde nije možda greška? U slučaju da od tih 10 mišonja svi prežive, Perica bi mogao izneti svih 10 degustiranih flaša. A u slučaju da jedan mišonja odapne, mogao bi izneti 999 flaša, jer bi tačno znao koja od tih 1000 je otrovna.
Nego, da li se u zadatku podrazumeva da je, u periodu od degustiranja vina pa do početka žurke, sasvim isključena mogućnost da neki od mišonja okonča prirodnom smrću, ili na bilo koji način koji nema veze sa otrovom?:-) Mislim, bilo bi malo opasno po goste na žurci ako Perica zbog smrti miša zaključi da je otrov u flaši iz koje je ovaj pio, a otrov zapravo negde drugde...:)
Šalu na stranu, da li sam na dobrom putu ako krenem sledećom strategijom:
1. miš degustira iz flaša sa rednim brojevima 1,2,3,4,...,100
2. miš degustira iz flaša sa rednim brojevima 2,4,6,8,...,200 (tj. prvih 100 brojeva deljivih sa 2)
3. miš degustira iz flaša sa rednim brojevima 3,6,9,12,...,300 (tj. prvih 100 brojeva deljivih sa 3)
4. miš degustira iz flaša sa rednim brojevima 4,8,12,16,...,400 (tj. prvih 100 brojeva deljivih sa 4)
5. miš degustira iz flaša sa rednim brojevima 5,10,15,20,...,500 (tj. prvih 100 brojeva deljivih sa 5)
6. miš degustira iz flaša sa rednim brojevima 6,12,18,24,...,600 (tj. prvih 100 brojeva deljivih sa 6)
7. miš degustira iz flaša sa rednim brojevima 7,14,21,28,...,700 (tj. prvih 100 brojeva deljivih sa 7)
8. miš degustira iz flaša sa rednim brojevima 8,16,24,32,...,800 (tj. prvih 100 brojeva deljivih sa 8)
9. miš degustira iz flaša sa rednim brojevima 9,18,27,36,...,900 (tj. prvih 100 brojeva deljivih sa 9)
10. miš degustira iz flaša sa rednim brojevima 10,20,30,40,...,1000 (tj. prvih 100 brojeva deljivih sa 10)
Nemam dokaz (za sada), ali po nekoj logici mi ovo izgleda kao najoptimalniji raspored?
Ovime ne bi bili pokriveni prosti brojevi između 101 i 1000, kao ni brojevi između 101 i 1000 koji nemaju faktore manje od 11.
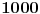 boca vina. Medjutim, tacno jedna od njih je otrovna. Pored boca, na raspolaganju su mu i
boca vina. Medjutim, tacno jedna od njih je otrovna. Pored boca, na raspolaganju su mu i 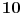 miseva kojima moze dati da degustiraju vino. Ukoliko neki mis popije iz otrovne boce, on ce tacno umreti pred zurku (naravno, jedan mis moze piti iz vise boca, ali ukoliko on umre vi necete znati zbog koje je flase preminuo). Pitanje je: koliko najvese boca mali Perica moze posluziti na zurku (znajuci naravno da nijedna od njih nije otrovna)?
miseva kojima moze dati da degustiraju vino. Ukoliko neki mis popije iz otrovne boce, on ce tacno umreti pred zurku (naravno, jedan mis moze piti iz vise boca, ali ukoliko on umre vi necete znati zbog koje je flase preminuo). Pitanje je: koliko najvese boca mali Perica moze posluziti na zurku (znajuci naravno da nijedna od njih nije otrovna)?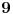 .
.



 [Zadatak] Logicki zadacic 2
[Zadatak] Logicki zadacic 2