Pretpostavljam da su sve tačke u istoj ravni, jer onda nema poligona.
Najpre treba da pronađeš ravan u kojoj se poligon nalazi. Za to možeš uzeti bilo koje tri tačke poligona (A, B, C) i izračunati normalu na ravan
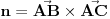
. Tačka A i normala n ti sada potpuno određuju ravan poligona. Vektori su predstavljeni kao matrice-kolone.
Sve koordinate transformišeš tako da se tačke poligona isprojektuju u jednu ravan, transformacijom čiji je inverz
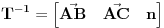
, dakle postaviš koordinatni sistem kome je jedna od tri koordinatne ravni upravo ravan poligona. Pritom AB i AC naravno nisu kolinearne jer inače ni nemaš poligon. Naravno odnos između apsolutnog koordinatnog sistema i ovog tvog je:
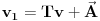
. U ovoj jednačini znaš koliko iznose A (to je vektor položaja tačke A) i znaš koliko iznosi T (mada je T dato preko odgovarajuće inverzne matrice).

je vektor položaja bilo koje tačke u koordinatnom sistemu koji ti je potreban (to treba da sračunaš!), a
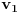
ti je (apsolutni) vektor položaja tačke koji znaš.
Treba da sračunaš za svaku tačku v_1:
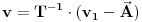
i dobijaš transformisane koordinate o kojima sam govorio.
Treća koordinata tačke koju ispituješ (nazovimo je X), dakle komponenta po vektoru normale n, posle transformacije treba da bude 0, inače tačka leži van ravni poligona pa dakle ni ne može biti u njemu.
Ako je dovde sve prošlo kako treba, primeniš Časlavov algoritam za utvrđivanje da li tačka pripada poligonu u ravni (potraži u starim porukama). Mislim da se radi samo o konveksnom poligonu, ali i to je bar nešto.
f