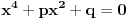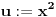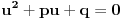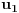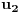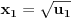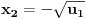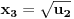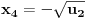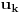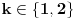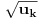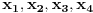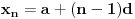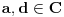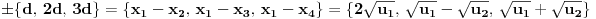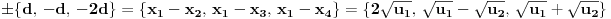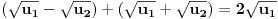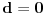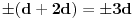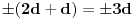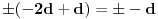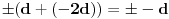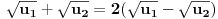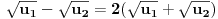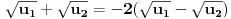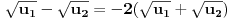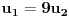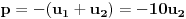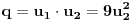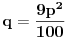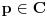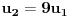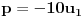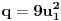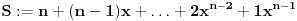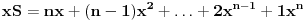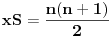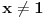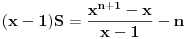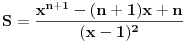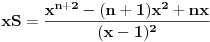1.
Jednačina
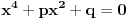
, nakon smene
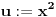
postaje
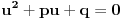
.
Neka su
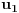
i
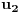
odgovarajuća rešenja.
Gubeći na strogosti (ali dobijajući na jednostavnosti zapisa

), možemo reći da su rešenja polazne j-ne data sa:
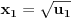
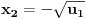
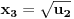
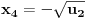 U slučaju da je neki od brojeva
U slučaju da je neki od brojeva 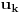 ,
, 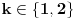 negativan ili kompleksan, izraz
negativan ili kompleksan, izraz 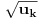 (za ovu priliku) treba tumačiti kao jednu (bilo koju) od 2 moguće kompleksne vrednosti.
(za ovu priliku) treba tumačiti kao jednu (bilo koju) od 2 moguće kompleksne vrednosti.
Kako brojevi
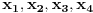
čine aritmetički niz
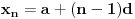
,
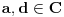
(naravno, ne obavezno u datom poretku) mora da važi:
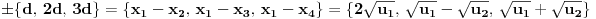
ili
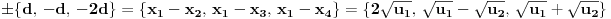 (ovo je skupovna jednakost, poredak elemenata u zapisu je nasumičan)
(ovo je skupovna jednakost, poredak elemenata u zapisu je nasumičan)
Vidimo da je
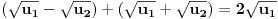
, pa ako zanemarimo slučaj
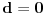
, jasno je da poslednja jednakost zapravo neka od sledećih:
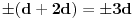
ili
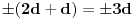
ili
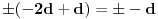
ili
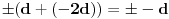
tj. mora biti
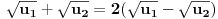
ili
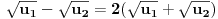
ili
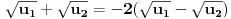
ili
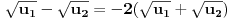
iz svakog od prva dva slučaja, nakon sređivanja dobijamo
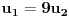
, pa na osnovu
Viète-ovih formula najzad imamo
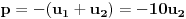
i
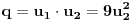
, pa je i tražena relacija
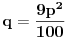
, pri čemu je
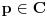
proizvoljno.
Iz svakog od druga dva slučaja dobijamo
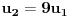
, pa kao i u prethodnim sledi
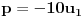
i
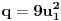
tj.
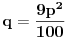
,
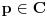
proizvoljno.
Naravno, ukoliko ne posmatramo kompleksne aritm. nizove, izvođenje je jednostavnije.
[Ovu poruku je menjao uranium dana 06.06.2007. u 07:50 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.




 Hitno - Dva zadatka za maturski
Hitno - Dva zadatka za maturski