Evo samo da javim da potraga za literaturom nije urodila plodom.
A ovo:
Citat:
uranium: Mislim da to pripada oblasti koja ima sledeće (
ravnopravne) nazive:
•
functional differential equations
•
difference-differential equations
•
differential-delay equations
nije baš sasvim tačno

Poslednja dva naziva zaista opisuju istu oblast iz koje sam pronašao gomilu literature, ali za ovaj problem nekorisne

jer se uglavnom odnosi na j-ne sa fiksnim pomakom.
[Ovu poruku je menjao uranium dana 14.09.2006. u 03:14 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
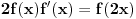 (rešenja su i
(rešenja su i 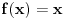 i
i 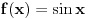 )? Razvijanjem u red? Ili postoje i druge taktike?
)? Razvijanjem u red? Ili postoje i druge taktike?