[es] - Furijeovi redovi

darkon
Darko Novakovic
Istrazivac, IMP
Beograd

Član broj: 13647
Poruke: 162
195.252.111.*

Jabber: darkon@elitesecurity.org

Profil

Re: Furijeovi redovi

^{17.05.2006. u 12:12}

Ti bi da razviješ aperiodičnu funkciju u Fourier-ov red?

Linkovi:
http://en.wikipedia.org/wiki/Fourier_series
http://planetmath.org/encyclopedia/FourierCoefficients.html
http://mathworld.wolfram.com/FourierSeries.html
http://mwt.e-technik.uni-ulm.d...mathematics/fourier/node2.php3
http://www.nst.ing.tu-bs.de/schaukasten/fourier/en_idx.html
http://www.sosmath.com/fourier/fourier1/fourier1.html

Ovo je i više nego dovoljno.

_{[Ovu poruku je menjao darkon dana 17.05.2006. u 13:17 GMT+1]}

_{[Ovu poruku je menjao darkon dana 17.05.2006. u 13:22 GMT+1]}

"Verovatno da preko nje mnoge sile kontrolišu mnogo šta..." - GANDOR
"Kada bi ljudski mozak bio tako jednostavan da bismo mogli da ga shvatimo, onda bismo mi bili toliko glupi da ga ipak ne bismo mogli shvatiti."

^{17.05.2006. u 12:12}

bierkof

Član broj: 11028
Poruke: 157
*.PPPoE-1709.sa.bih.net.ba.

Profil

Re: Furijeovi redovi

^{17.05.2006. u 21:50}

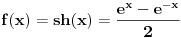
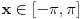
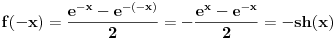
iz ovoga zakljucujemo da je funkcija neparna.... sto automatki povlaci:

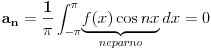
Ovime je i prvi clan :

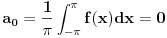
dalje je...

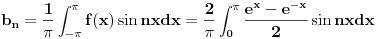
Dalje znamo da je....

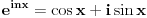
sto cemo iskoristiti na ovaj nacin....

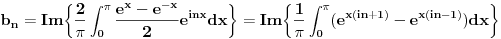
Ovi integrali nisu bas toliko teski, sada.... Prvo cu da ih rijesim (smijena ti je

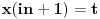
kod prvog, analogno kod drugog) pa cu onda da uvodim granice... Sada se dobije (nakon sabiranja i racionalizacije):

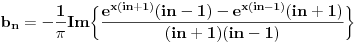
sada ovo sve napises u ovom obliku

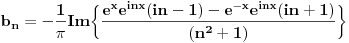
Ponovo vracas onu kompleksnu smjenu (Ojlerov obrazac)

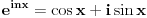
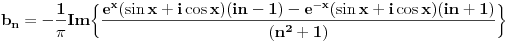
Malo to sredis i uvrstavas granice.... dobije ovo (odmah sam brisao realne djelove kod mnozenja kompl. brojeva, nemoj bas sve da kucam :) ):

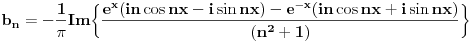
Sada granice, uglavnom, kad uvrstis donju dobijes nulu, oslobodis se imaginarne jedinice i ostavis samo im. dio kompl. broja, donju granicu preskacem, za gornju imas ovo:

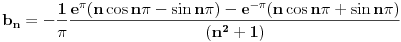
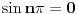
je uvjek nula za n=1,2,3,....

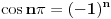
za n=1,2,3,.... (nacrtaj trigonometrijsku kruznicu pa ces vidjeti....)

sada nas koeficjent b izgleda ovako:

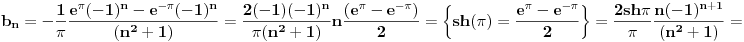
I to je gotovo sada tvoj furierov red izgleda ovako:

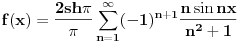
Nadam se da sam pomogao, ako jos nesto bude trebalo reci, ukoliko budem u stanju odgovorit cu ti....

edit:

ispravljenja greska u kucanju

_{[Ovu poruku je menjao bierkof dana 17.05.2006. u 23:11 GMT+1]}

Guybrush Threepwood: How much wood could a woodchuck chuck if a woodchuck could chuck wood?
Woodsmith: A woodchuck could chuck no amount of wood since a woodchuck can't chuck wood
Guybrush Threepwood: But if a woodchuck could chuck and would chuck some amount of wood, what amount of wood would a woodchuck chuck?

^{17.05.2006. u 21:50}

darkon
Darko Novakovic
Istrazivac, IMP
Beograd

Član broj: 13647
Poruke: 162
*.rcub.bg.ac.yu.

Jabber: darkon@elitesecurity.org

Profil

Re: Furijeovi redovi

^{18.05.2006. u 07:48}

Eto ti sad!
Ili su mene pogresno učili, ili se teorija Fourier'ovih redova u međuvremenu promenila....

^{18.05.2006. u 07:48}

bierkof

Član broj: 11028
Poruke: 157
*.PPPoE-2505.sa.bih.net.ba.

Profil

Re: Furijeovi redovi

^{18.05.2006. u 13:48}

Koliko ja znam nije se ništa u medjuvremenu promjenilo, bar ne poslije 1986-te pošto ja učim iz Uščumlića 2 koji je tada izdat :)

Predpostavljam da mislis na ono što si rekao da je sh(x) aperiodična funkcija...

Da bi funkciju bili u stanju da razvijemo u furierov red, na nekom intervalu potrebno je da zadovoljava Dirichleove uslove na tom intervalu:
1) Uniformno ogranicena tj.

za svako

gdje je M konstanta
2) Ima konačno mnogo tačaka prekida i svi su prvog reda, tj. postoji konačan lijevi i desni limes u svakoj tacki prekida
3) Ima ne više od konačnog broja pravih ekstrema.

Ako funkcija zadovoljava Dirichleove uslove tada se za svaku tačku x tog intervala za koju je

gdje je

ona može predstaviti Furierovim redom.

Pošto sam vidio da te zbunilo to sa sh(x), ona jeste aperiodična funkcija ali mi učinimo da bude periodična... Ako funkcija f nije periodična onda se njena restrikcija ili sama ona može periodično produžiti do funkcije

Ili obicnim jezikom... Nacrtaj dijagram sh(x), uzmi dio između

i ponovi isti taj dio nakon prvog

, i tako produži funkciju na cijelom skupu R, dobio si periodičnu funkciju neku

sa periodom

... koja zadovoljava Dirichleove uslove, tada mozes da tu funkciju prikažeš Furierovim redom.

Isto tako je za

ili za

.

_{[Ovu poruku je menjao bierkof dana 18.05.2006. u 14:52 GMT+1]}

^{18.05.2006. u 13:48}

darkon
Darko Novakovic
Istrazivac, IMP
Beograd

Član broj: 13647
Poruke: 162
*.rcub.bg.ac.yu.

Jabber: darkon@elitesecurity.org

Profil

Re: Furijeovi redovi

^{18.05.2006. u 14:42}

Citat:

Pošto sam vidio da te zbunilo to sa sh(x), ona jeste aperiodična funkcija ali mi učinimo da bude periodična

Ma ništa mene nije zbunilo...Samo je ovo trebalo naglasiti u samoj postavci zadatka.
Sada se zna kako izgleda funkcija.
Furijeova red funkcije

na intervalu

je prilično neodređena formulacija.

^{18.05.2006. u 14:42}