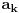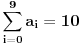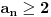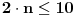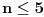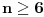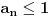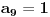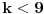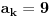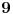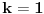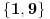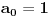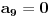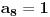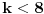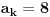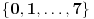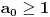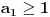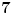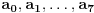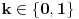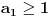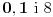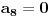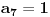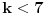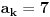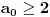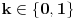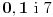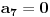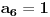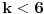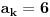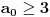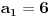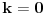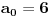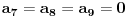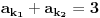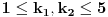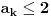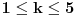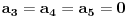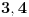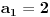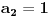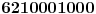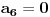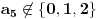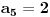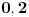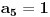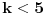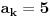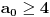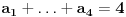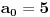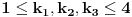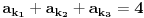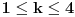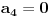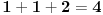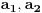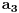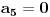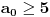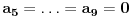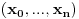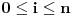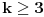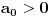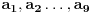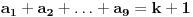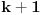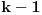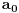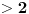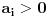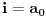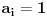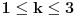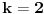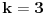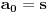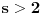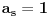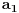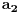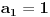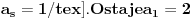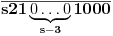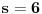Radi jednostavnosti, koristiću ipak sledeće oznake:

, gde je
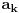
broj pojavljivanja cifre

u dekadnom zapisu traženog broja.
Jasno je da mora biti
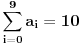
.
Primetimo zatim da ako je
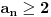
imamo da postoje barem dve
različite cifre koje se pojavljuju po

puta, ali cifara u zapisu ima samo
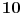
, pa mora biti
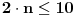
tj.
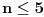
.
Drugim rečima, za
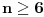
je
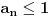
.
Ako bi bilo
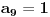
, onda bi postojalo
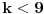
takvo da je
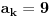
. Međutim, ovo poslednje bi značilo da imamo,
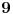
cifara

, pa lako sledi da mora biti
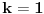
(za preostalih

ne možemo staviti cifru van skupa
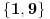
, jer nam treba
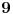
istih cifara, pa zbog
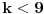
sledi da je
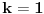
). Sada, je lako videti da smo dobili broj koji ne zadovoljava uslove zadatka (npr. dobijamo da je
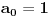
a u zapisu nema ni jedna

) pa je to kontradikcija.
Dakle, mora biti
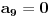
Ako bi bilo
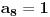
, onda bi postojalo
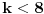
takvo da je
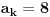
. Ovo poslednje implicira postojanje tačno

pojavljivanja neke od cifara
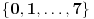
. Budući da je
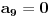
i po pretpostavci
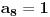
imamo da je
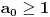
i
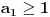
, sledi da moramo staviti da je nekih
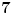
od cifara
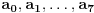
međusobno jednako, pa mora biti
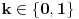
, a otuda sledi (zbog
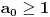
i
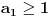
) da u zapisu ipak ne učestvuju samo cifre
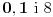
, što je kontradikcija.
Dakle, mora biti
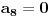
Ako bi bilo
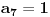
, onda bi postojalo
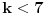
takvo da je
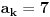
. Na osnovu prethodnih zaključaka i na osnovu pretpostavke, važi
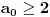
i
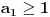
, slično kao i ranije zaključujemo da moramo uzeti da je
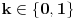
. Međutim, šta god uzeli za

, dobićemo da su cifre

pozitivne, što znači da cifre
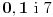
nisu jedine u zapisu, a to je kontradikcija.
Dakle, mora biti
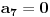
Neka je
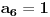
, onda postoji
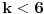
takvo da je
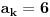
. Iz prethodnih razmatranja sledi da je
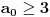
i
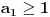
. Kao i ranije, sledi da je
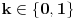
. Ali, ne može biti
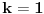
tj.
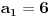
, jer bi zbog
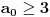
i
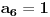
morali da za preostale

cifre

stavimo

jedinica, što je nemoguće. Dakle, mora biti
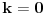
tj.
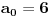
.
Ostaje nam da otkrijemo cifre

. Iz
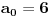
i
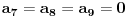
sledi da su među ciframa

tačno tri jednake

, tj. tačno dve cifre nisu nula. Kako je
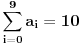
iz prethodnog sledi, da je
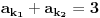
za neke
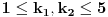
. Sada imamo da je
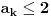
za
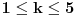
. Odatle, vidimo da mora biti
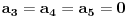
, jer bi u protivnom dobili da se neka od cifara

javlja
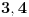
ili

puta (što je kontradikcija).
Sada, je lako proveriti da je
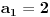
i
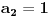
.
Dakle, dobili smo broj
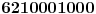
.
Dokažimo da je nađeni broj jedinstven.
Za sada znamo da je
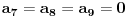
. Pretpostavimo zato da je
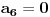
.
Očigledno je da je

. Međutim, videćemo ubrzo da
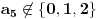
, što će biti dovoljno za dokaz jedinstvenosti trženog broja.
Ako bi bilo
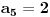
, sledilo bi da postoje dva pojavljivanja cifre

u zapisu, što znači da se neke dve različite cifre pojavljuju po

puta u zapisu, što je kontradikcija, jer smo dobili da u zapisu učestvuju cifre
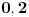
i

.
Ako bi bilo
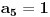
, sledilo bi da postoji
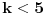
takvo da je
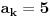
, kao i ranije, (zbog
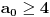
i
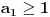
) mora biti
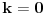
. Sada, sledi da je
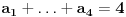
, a pošto je
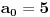
, među sabircima je tačno jedna

, onda za neke
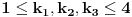
važi
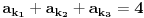
, pa je
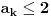
za
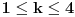
. Znači, mora biti
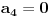
(u protivnom bi se neka od cifara

javljala

puta, što je kontradikcija). E sad, jedina particija broja

, koja zadovoljava tražene uslove je
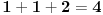
, međutim, kako god dodelili te brojeve ciframa
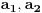
i
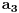
, dobijamo da u zapisu učestvuju ukupno

jedinice, a

, što je kontradikcija.
Ako bi bilo
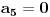
, sledilo bi
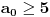
, što je u kontradikciji sa
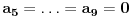
.
Bez obzira što je rešenje ovako ružno, mislim da je zadatak fantastičan, jer pokazuje kakvi se perverzni skupovi kriju u

.
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
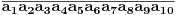 ,
, 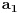 je broj nula u dekadnom zapisu tog broja,
je broj nula u dekadnom zapisu tog broja, 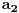 je jednak broju jedinica u zapisu, itd.,
je jednak broju jedinica u zapisu, itd., 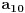 je jednak broju devetki. Odrediti taj broj.
je jednak broju devetki. Odrediti taj broj.



 Simpatičan zadačić
Simpatičan zadačić