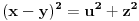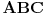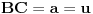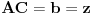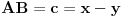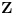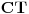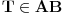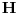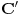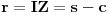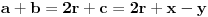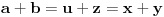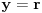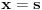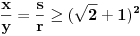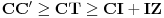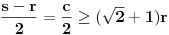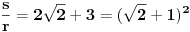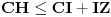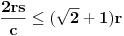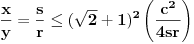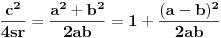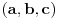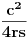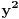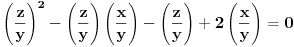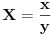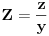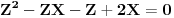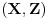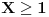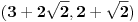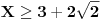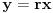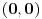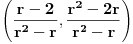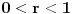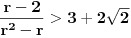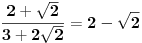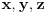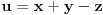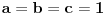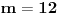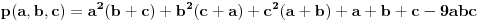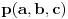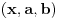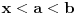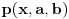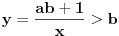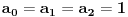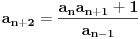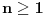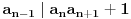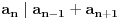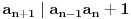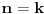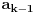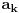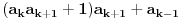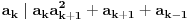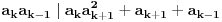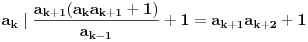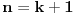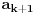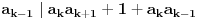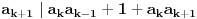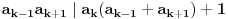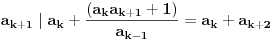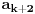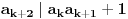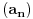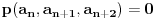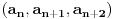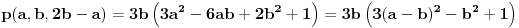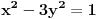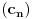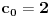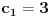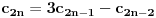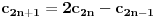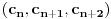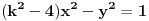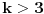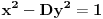 ,
,gde je
 ma koji prirodan broj koji nije potpun kvadrat. Ukoliko se na desnoj strani jednačije nalazi broj različit od 1, onda se takva jednačina naziva jednačinom Pelovog tipa, i o njoj nešto više reči kasnije.
ma koji prirodan broj koji nije potpun kvadrat. Ukoliko se na desnoj strani jednačije nalazi broj različit od 1, onda se takva jednačina naziva jednačinom Pelovog tipa, i o njoj nešto više reči kasnije.Ono što je bitno napomenuti je da svaka Pelova jednačina ima beskonačno mnogo rešenja. Ukoliko pronađemo jedno od njih
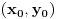 preostala možemo generisati rekurentnim relacijama:
preostala možemo generisati rekurentnim relacijama: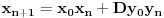
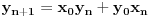
Tu je i gotova formula:
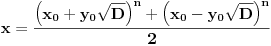
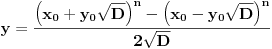
Međutim, problem koji se pojavljuje je taj što je ponekad (zapravo, skoro uvek) vrlo teško pronaći i jedno rešenje date jednačine. Na sreću, postoji metod koji se može koristiti, i on ne samo što pronalazi jedno rešenje date jednačine već je to rešenje minimalno, tako da se gore opisanim formulama mogu generisati sva moguća rešenja. Evo kako izgleda taj metod:
Cilj nam je da nađemo continued fraction (nisam siguran za prevod ovog izraza), čija je vrednost jednaka
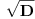 . Kada to uspemo jednačina je praktično rešena. Postupamo na sledeći način:
. Kada to uspemo jednačina je praktično rešena. Postupamo na sledeći način:Neka je
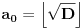
Sada imamo
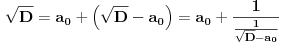
Primenimo istu proceduru na
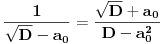 i imamo
i imamo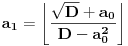
Sada je
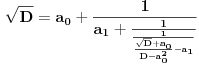 , pa sledi da je
, pa sledi da je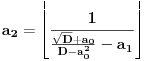
Nastavljamo da na ovaj način računamo elemente niza. U jednom momentu dobićemo ovako nešto:
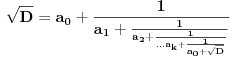 . Tad treba stati. Ako je
. Tad treba stati. Ako je  neparan broj onda je minimalno rešenje jednačine par uzajamno prostih brojeva takvih da je
neparan broj onda je minimalno rešenje jednačine par uzajamno prostih brojeva takvih da je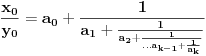 .
.Za parno
 važi
važi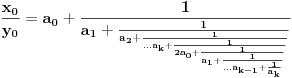
Evo i primera kako to izgleda:
Neka je potrebno rešiti jednačinu
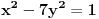 . Postupamo po datom uputstvu:
. Postupamo po datom uputstvu: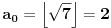
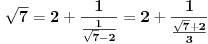
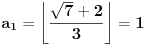
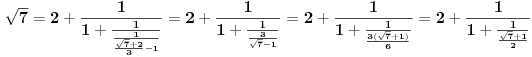
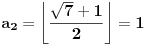
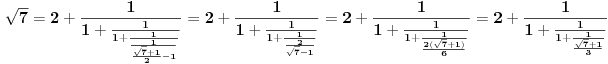
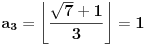
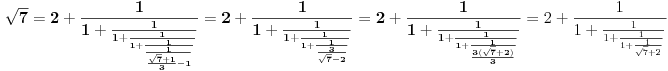
Zaključujemo (na osnovu gore navedenog) da ovde treba stati. Pošto je poslednji izračunat element
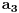 sa neparnim koeficijentom, najmanje rešenje jednačine je sledeće:
sa neparnim koeficijentom, najmanje rešenje jednačine je sledeće: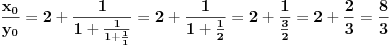 , odnosno
, odnosno 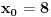 ,
, 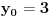 .
.Evo i jednog drugačijeg primera, shvatićete na kraju (ako izdržite dotle :)) zašto je drugačiji:
Neka je data jednačina
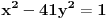 . Računamo elemente niza kao i u prethodnom slučaju:
. Računamo elemente niza kao i u prethodnom slučaju: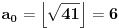
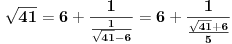
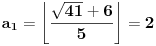
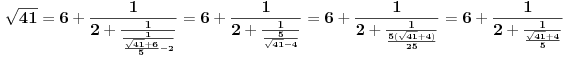
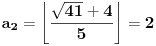

Dakle, ovde treba stati. Razlika u odnosu na prethodni primer je što je ovog slučaja poslednji izračunat član niza sa parnim koeficijentom (
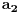 ). Znači, najmanje rešenje se traži nešto drugačije:
). Znači, najmanje rešenje se traži nešto drugačije: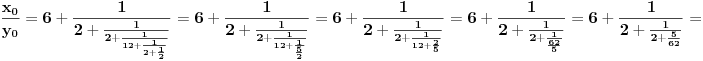
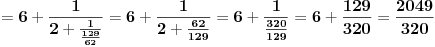 odnosno
odnosno 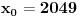 ,
, 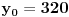 (mora se priznati, rešenje koje bi se vrlo teško našlo nekom drugom metodom).
(mora se priznati, rešenje koje bi se vrlo teško našlo nekom drugom metodom).Sva preostala rešenja ovih dveju jednačina dobijamo opisanim relacijama.
[Ovu poruku je menjao Bojan Basic dana 15.01.2007. u 15:18 GMT+1]




 Rešavanje Pelove jednačine
Rešavanje Pelove jednačine
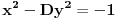
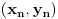
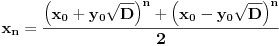
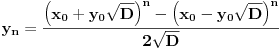

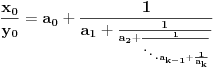
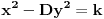
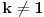
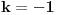
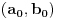
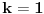
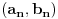
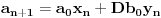
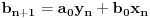
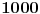
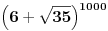
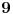
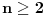

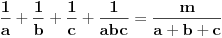
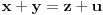
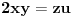
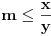
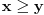
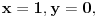
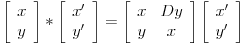
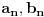
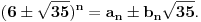
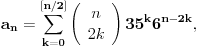
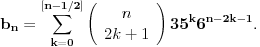
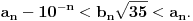
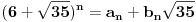
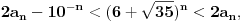
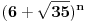
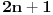


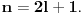
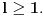
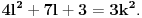
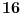
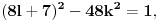
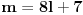
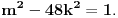
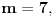
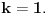
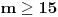
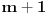
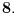

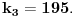
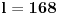
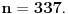
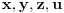
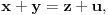
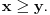
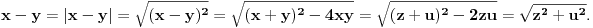
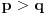
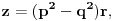
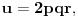
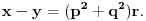
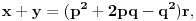
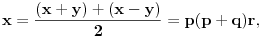
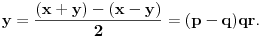
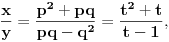
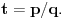


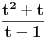
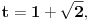
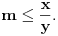
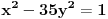
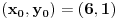

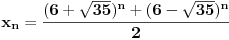
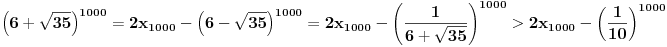
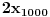
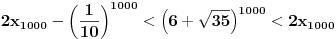
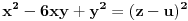
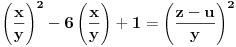
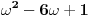
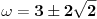
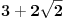
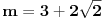
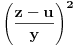

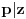
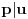
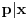
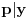


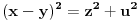



 Re: Rešavanje Pelove jednačine
Re: Rešavanje Pelove jednačine