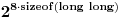[es] - Neko ljubazan da mi prevede kod ?

pirgos_madden
Pirgos Madden
Pirot

Član broj: 16752
Poruke: 322
195.252.107.*

Jabber: Programing
Sajt: www.pirot-mafia.co.sr

Profil

Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 17:43 - pre 248 meseci}

Kako nisam mnogo vican C-u i ne programiram mnogo u njemu moze li neko sledeci kod

Code:

main(){int a[9000000],i=9e6,n=i,p=1;while(--i)a[i]=1;
while(++p<n)for(a[p]?printf("%d ",i=p):0;p<4e4&&i*p<n;a[i++*p]=0);}

da mi "prevede" na "normalni" C - kod, dakle bez ovih skracenica u vidu upitnika, zvezdica, pluseva (dobro ovo moze) i ostalih zezalica (moze ga slobodno napisati sa prelaskom u novi red i sa razmacima - dakle po pravilima "lepog" tj. razumljivog pisanja koda).
Hvala!

-I srusise se nasi divni snovi !!!
-NATO is bombing Serbia, a Yugoslavian republic, to stop the Serbs from forcing ethnic Albanians from Kosovo. Serb supporters sock it to NATO, U.S. Web sites. Magis says NATO headquarters won't launch an electronic counterstrike. "We want to show we're more civilized," he says. "We believe in freedom of speech." NATO is even discussing the possibility of hosting Serbian information on the Web so the Serbs can share their views.

Odgovor na temu

Not now, John!

Član broj: 231
Poruke: 1318
*.dialup.blic.net.

+4 Profil

Re: Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 18:50 - pre 248 meseci}

Kôd je baš smiješan :-)
Ovo je neki mazohista pisao.

Code:

main() {
  int a[9000000], i=9e6, n=i, p=1; // definiše varijable (a je vektor od 9000000 elemenata, i=9000000)
  while (--i) a[i]=1; // svi elementi vektora a, osim a[0] su jednaki 1
  while (++p<n) // za vrijednoti p=2, 3, 4, ... 8999999 radi sljedeću petlju:
    for (a[p] ? printf("%d ",i=p) : 0; p<4e4 && i*p<n; a[i++*p]=0); // (ovo mi se ne da tumačiti, možda neko bude imao više živaca)
}

"I'd take the awe of understanding over the awe of ignorance any day."
- Douglas Adams

Odgovor na temu

Alef
Viktor Kerkez
Novi Sad

Član broj: 505
Poruke: 188
*.150.EUnet.yu.

Profil

Re: Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 19:01 - pre 248 meseci}

Ovaj kod ti, kao što si već verovatno i primetio

ispisuje sve proste brojeve, a koristi algoritam Eratostenovog sita.

1) Pošto ispisuje sve proste brojeve do 9.000.000 treba mu niz od 9.000.000 elemenata i par brojača.

Code:

int a[9000000], i = 9000000, n = i, p = 1;

2) Onda predpostavi da su svi prosti, tj. svakom elementu niza dodeli jedinicu, pošto će ispisivati samo one brojeve za čije pozicije se u nizu nalazi jedinica.

Code:

while (--i) a[i] = 1;

3) E sad, pošto je p postavljeno na jedinicu, a operator ++ je prefiksni, onda će prvo da poveća p za 1 pa tek onda da ga uporedi sa n, što u prevodu znači, da p polazi od 2, što nam i treba, jer je 2 prvi prost broj. I tu ustvari ulazimo u petlju za ispisivanje prostih brojeva od 2 do 9.000.000, jer je n, na početku postavljeno na 9.000.000.

Code:

while((++p) < n) {

4) E sad…

Code:

for(a[p]?printf("%d ", i = p):0; p < 45000 && i*p < n; a[i++ * p] = 0);

U ovoj petlji je brojač i. Na početku u izrazu za inicijalizaciju, proverimo da li je broj p prost i ako jeste ispišemo ga. I usput dodelimo brojaču vrednost p.

Code:

a[p]?printf("%d ", i = p):0; <=> if (a[p] == 1) { printf("%d ", p); i = p; }

Ova for petlja u suštini eliminiše sve umnoške datog broja p od njegovog kvadrata do 9.000.000 (postavi u nizu a na njihovo mesto 0). Umnošci manji od kvadrata su eliminisani u ranijim petljama.

Code:

a[(i++) * p] = 0

I petlja se vrti sve dok p*i ne postane veće od n (sve dok ne probijemo 9.000.000). Prvi uslov je postavljen da ne bi probili granice integer-a kada množimo i*p, u suštini smo mogli staviti i p < sqrt(9.000.000) jer za veće brojeve nema smisla raditi eliminaciju.

I to bi otprilike bilo to… A kada se sve sastavi dobijemo…

Code:

#include <stdio.h>

int main(){
    int a[9000000], i = 9000000, n = i, p = 1;

    while (--i) a[i] = 1;

    while((++p) < n) {
        if (a[p] == 1) printf("%d ", p);
        for(i = p; p < 3000 && i*p < n; a[(i++) * p] = 0);
    }
    return 0;

}

Odgovor na temu

pirgos_madden
Pirgos Madden
Pirot

Član broj: 16752
Poruke: 322
195.252.107.*

Jabber: Programing
Sajt: www.pirot-mafia.co.sr

Profil

Re: Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 19:13 - pre 248 meseci}

Citat:

Not now, John!: Kôd je baš smiješan :-)
Ovo je neki mazohista pisao.
]

Pa da, tako nesto, to sam nasao na elitesecurity-ju:
www.elitesecurity.org/tema/51140
prilicno je zanimljivo.

Citat:

Alef: Ovaj kod ti, kao što si već verovatno i primetio ispisuje sve proste brojeve, a koristi algoritam Eratostenovog sita

Pa da, "oduvek" kad mi je trebalo da trazim neke proste brojeve padalo mi je na pamet da to probam sa Eratostenovim sitom ali mi se cinilo da ce jako sporo raditi obzirom da se vrti po "ugnjezdenoj" petlji tako da nisam ni probao. Bas sam se "obradovao" kad nadjoh to na pomenutom sajtu.

Odgovor na temu

pirgos_madden
Pirgos Madden
Pirot

Član broj: 16752
Poruke: 322
195.252.107.*

Jabber: Programing
Sajt: www.pirot-mafia.co.sr

Profil

Re: Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 19:38 - pre 248 meseci}

Imam jos par pitanja. Eto sto se tice tog niza:

Code:
int a[9000000]

Do koliko ga je moguce budziti? Da li postoje ogranicenja i kako se mogu zaobici?

Sto se tice sledeceg

Code:
while (--i) a[i] = 1;

da li se to moze uraditi "u jednom potezu" odnosno da se jednom komandom, bez while petlje, kaze da se niz inicijalizuje nekim vrednostima?

Odgovor na temu

Alef
Viktor Kerkez
Novi Sad

Član broj: 505
Poruke: 188
*.84.EUnet.yu.

Profil

Re: Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 20:22 - pre 248 meseci}

Citat:

pirgos_madden: Imam jos par pitanja. Eto sto se tice tog niza:

Code:
int a[9000000]

Do koliko ga je moguce budziti? Da li postoje ogranicenja i kako se mogu zaobici?

Pa u principu možeš koliko god imaš memorije, ali ako je sam alociraš memoriju sa malloc. Meni gcc iskompajlira nizove veće od 1.000.000 članova, ali mi program pukne čim ga pokrenem.

Ustvari kada malo bolje razmislim možeš samo do

Citat:

Code:
while (--i) a[i] = 1;

da li se to moze uraditi "u jednom potezu" odnosno da se jednom komandom, bez while petlje, kaze da se niz inicijalizuje nekim vrednostima?

Mislim da ne može, ali nisam siguan.

Odgovor na temu

Marko Stankovic

Član broj: 11
Poruke: 306
*.rvkds.net.

Profil

Re: Neko ljubazan da mi "prevede" kod ?

^{24.11.2004. u 21:42 - pre 248 meseci}

Mozes nizu da dodelis vrednosti bez problema, recimo to se radi ovako:

int a[5]={1,2,3,4,5};

ili ako oces da napunis niz nulom dovoljno je samo da stavis tu vrednost:

int a[5]={0}

naravno mozes da punis i matrice recimo ovako:

int a[2][2]={{1,2},{3,4}};

ako navedes samo prvih par vrednosti on ce ih ubaciti u niz a ostalo ce popuniti nulama ako me pamcenje ne vara, znaci ovako:

int a[5]={2,3}

elementi niza ce biti:
2 3 0 0 0

E sada naravno u ovom zadatku se koristi while petlja jer je malo glupo da navedes 9000000 vrednosti iza znaka jednakosti.

Inace ako volite ovakve perverzije imam jedan zadacic koji sam iskopao odavno na netu, taj kod je valjda pobedio na nekom takmicenju ili sta vec. Evo kod pa se zanimajte da protumacite:

Code:

#include <stdio.h>

main(t,_,a)
char *a;
{return!0<t?t<3?main(-79,-13,a+main(-87,1-_,
main(-86, 0, a+1 )+a)):1,t<_?main(t+1, _, a ):3,main ( -94, -27+t, a
)&&t == 2 ?_<13 ?main ( 2, _+1, "%s %d %d\n" ):9:16:t<0?t<-72?main(_,
t,"@n'+,#'/*{}w+/w#cdnr/+,{}r/*de}+,/*{*+,/w{%+,/w#q#n+,/#{l,+,/n{n+\
,/+#n+,/#;#q#n+,/+k#;*+,/'r :'d*'3,}{w+K w'K:'+}e#';dq#'l q#'+d'K#!/\
+k#;q#'r}eKK#}w'r}eKK{nl]'/#;#q#n'){)#}w'){){nl]'/+#n';d}rw' i;# ){n\
l]!/n{n#'; r{#w'r nc{nl]'/#{l,+'K {rw' iK{;[{nl]'/w#q#\
n'wk nw' iwk{KK{nl]!/w{%'l##w#' i; :{nl]'/*{q#'ld;r'}{nlwb!/*de}'c \
;;{nl'-{}rw]'/+,}##'*}#nc,',#nw]'/+kd'+e}+;\
#'rdq#w! nr'/ ') }+}{rl#'{n' ')# }'+}##(!!/")
:t<-50?_==*a ?putchar(a[31]):main(-65,_,a+1):main((*a == '/')+t,_,a\
+1 ):0<t?main ( 2, 2 , "%s"):*a=='/'||main(0,main(-61,*a, "!ek;dc \
i@bK'(q)-[w]*%n+r3#l,{}:\nuwloca-O;m .vpbks,fxntdCeghiry"),a+1);
{
scanf(0);
}
;
;}

I drink to make other people interesting.

Odgovor na temu