Pre svega, primetio sam popriličnu rupu u postavci. Naime, rotacija ti nije dobro definisana: kažeš da rotiramo sto oko njegove ose, a tu osu ne možeš odrediti ako sto ne stoji sa sve četiri noge na zemlji (jer se sto onda „gega“, i postavlja se pitanje koji od tih položaja odabrati kao merodavan za određivanje ose). Ipak, pošto u istoj rečenici u kojoj objašnjavaš rotiranje osu nazivaš
vertikalnom (iako je ona vertikalna samo u vrlo specijalnom slučaju, kada je ravan stola horizontalna), pretpostavljam da si se samo nespretno izrazio, i da zapravo želiš rotaciju oko vertikalne prave koja prolazi kroz centar kvadrata određenog podnožjima nogu. Ostatak poruke napisan je podrazumevajući ovo tumačenje, a ti ćeš me već ispraviti ako si mislio na nešto drugo.
Citat:
Fitopatolog:
Ako pretpostavimo da podovi u našim kafićima nemaju udubljenja i ispupčenja sa vertikalnim i veoma strmim stranama već su strmine vrlo blage (što je razumna pretpostavka za većinu naših kafića), tada se naš prethodni slučaj unekoliko menja. Da li u takvoj situaciji možemo naći položaj stola u kome se on ne gega?
Drugim rečima, pooštravaš uslove tako što zahtevaš da funkcija koja oslikava udubljenje bude neprekidna. U tom slučaju
možemo rotacijom za pogodan ugao postići da se sto ne „gega“.
Pre svega, treba ustanoviti uslov koji garantuje da se sve četiri noge oslanjaju na pod (u zavisnosti, naravno, od dubina/visina poda pod nogama — označimo ih sa

,

,

i

, ciklično). Pretpostavimo da sto stoji stabilno. Podnožja sve četiri noge nalaze se u temenima jednog kvadrata, čiji ćemo centar obeležiti sa

. Obeležimo još sa

tačku koja ima

i

koordinate iste kao i tačka

, i

koordinatu jednaku

. Posmatrajmo sada vertikalnu ravan određenu tačkama u kojima dve međusobno naspramne noge dodiruju pod. Duž
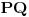
možemo posmatrati kao srednju liniju jednog pravouglog trapeza u toj ravni: njegove osnovice protežu se od dodirnih tačaka nogu i poda do ravni
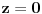
. U zavisnosti od toga koji smo par naspramnih nogu posmatrali, dobijamo
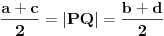
, te je potreban uslov da sve četiri noge dodiruju pod upravo
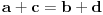
. Ovaj uslov je i dovoljan, jer je ravan jednoznačno određena trima nekolinearnim tačkama, te uvek možemo proizvoljno odabrati tri vrednosti i četvrta je odmah određena.
Dakle, ako u početnom momentu sto nije stabilan, možemo pretpostaviti, bez umanjenja opštosti, da važi
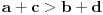
. Rotirajmo sto za četvrtinu kruga; veličine

,

sada su zamenile vrednosti s veličinama

,

, međusobno, te se znak u navedenoj nejednakosti okrenuo. Međutim, zbog neprekidnosti funkcije koja oslikava udubljenje, i funkcija
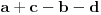
(u zavisnosti od ugla rotacije) takođe je neprekidna. Kako je u polaznom momentu njena vrednost pozitivna, a u krajnjem negativna, prema teoremi o srednjoj vrednosti ova funkcija ima nulu, tj. bar u jednom momentu važi jednakost
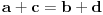
, i tada je sto stabilan. Ovim je dokaz završen.
Citat:
Fitopatolog:
Dodatno potanje je da li se isto može postići ako vrhovi nogu stola ne pripadaju jednoj istoj ravni?
Odgovor na ovo pitanje nešto je jednostavniji: ne može, što pokazuje primer potpuno ravnog poda.

Ljubičice crvena, što si plava kô zelena trava.