Citat:
petarm: Fje stanja u kvantnoj mehanici su mi elementi Hilbertovog prostora. Medjutim kod ravnih talasa imam slusaj da mi integral divergira, te moram da prosirim Hilbertov prostor i normiram integral na
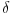
funkciju. Da li sam ja iz Hilbertovog prostora izasao u prostor temperiranih distribucija?
Ne možeš baš da normiraš integral na delta funkciju, zato što je norma po definiciji realan broj, a ne funkcija, a btw, delta funkcija i nije funkcija (u užem smislu). Delta funkcija služi za proširenje notacije ortogonalnosti i na beskonačnodimenzionalne prostore stanja.
Što se ravnih talasa tiče, važi ono što je kolega Milošević rekao: oni su idealizacija, ali iz njihove norme se ipak može izvući fizički relevantan zaključak. Naime, neka je dat ravni talas
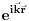
, proizvoljna tačka u konfiguracionom prostoru
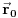
i neka zapremina
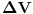
centrirana oko
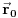
. Odavde onda imamo da je verovatnoća nalaženje čestice opisane pomenutim ravnim talasom u pomenutoj zapremini
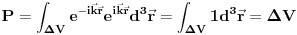
. Odavde vidimo da se čestica može naći u sa jednakom verovatnoćom u svim delovima prostora sa istom zapreminom, ili alternativno, ako pustimo da
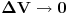
da se čestica može naći podjednako verovatno u svim tačkama prostora sa verovatnoćom 0.
Pošto je sistem koji opisujemo uvek ograničen na neki prostor linearne dimenzije L, u praksi nećemo imati posla sa ravnim, nego sa stojećim talasima koji imaju dobro definisanu normu, tj. dominantni model je model čestice u kutiji.
edit: Za petra: Talasni paket ne opisuje česticu u kutiji, nego lokalizovanu česticu.
[Ovu poruku je menjao tomkeus dana 10.11.2007. u 02:12 GMT+1]
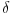 funkciju. Da li sam ja iz Hilbertovog prostora izasao u prostor temperiranih distribucija?
funkciju. Da li sam ja iz Hilbertovog prostora izasao u prostor temperiranih distribucija?