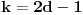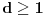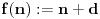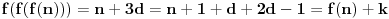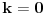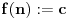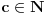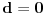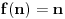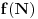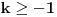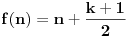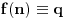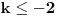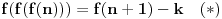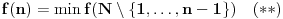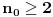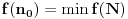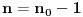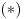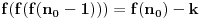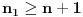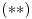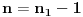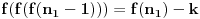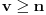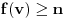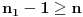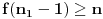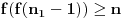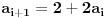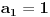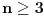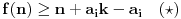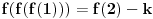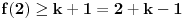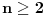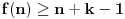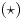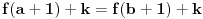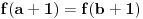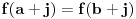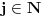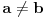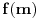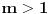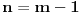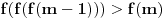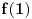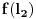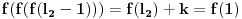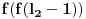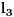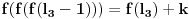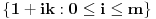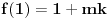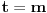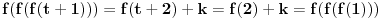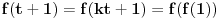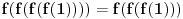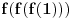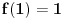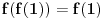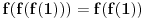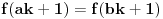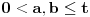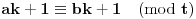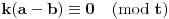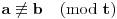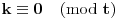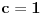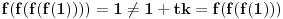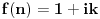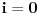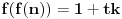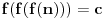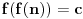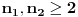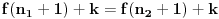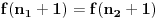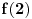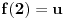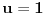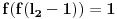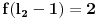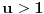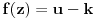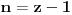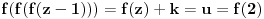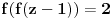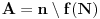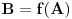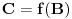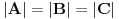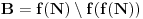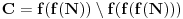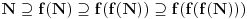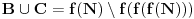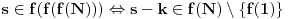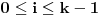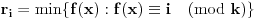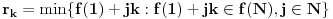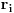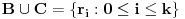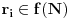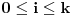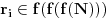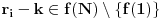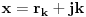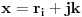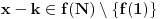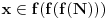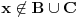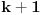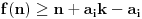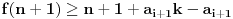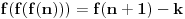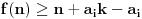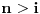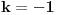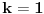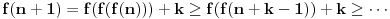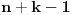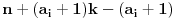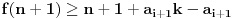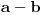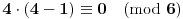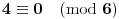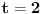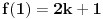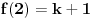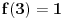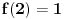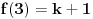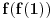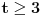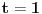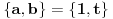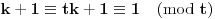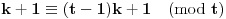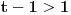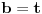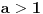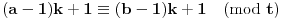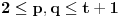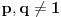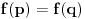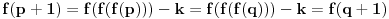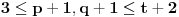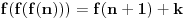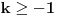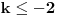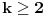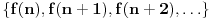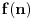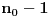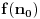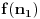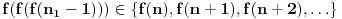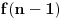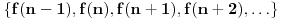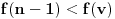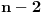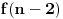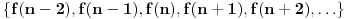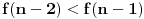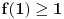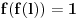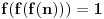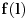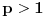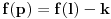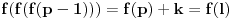Još veći napredak - konačno sam rešio zadatak! Mislim da je ovo definitivno zadatak koji me je najviše izmučio ikada, ali sad mu je došao kraj.
Nadam se da se niko neće ljutiti što odmah objavljujem rešenje umesto da još malo sačekam, ali ipak, možda je neko već i probao da ga uradi pa nije uspeo, ko hoće još malo da se muči sam neka još ne čita ovo što ću napisati, a ja sam nestrpljiv da podelim ovo, po mom (neskromnom) mišljenju, zaista sjajno rešenje. Samo da napomenem da ćete verovatno videti nebulozne tehnike koje nijedna normalna osoba ne koristi prilikom rešavanja funkcionalnih jednačina, ali eto ja ih koristio :) Dakle, svi vi koji hoćete još malo da pokušavate sami ovo je pravi momenat da prestanete sa čitanjem, svi ostali nastavite :)
Najpre navodim rezultat:
Data funkcionalna jednačina ima rešenja za i samo za neparne
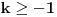
i za
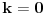
.
Rešenje ide u 3 dela.
1) Neparno
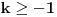
ili
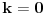
.
Kolega uranium je ovo već napisao, ali ponoviću kompletnosti radi. U ovom slučaju funkcionalna jednačina ima jedno rešenje
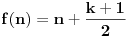
za neparno
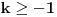
, odnosno
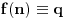
(

je proizvoljna konstanta) za
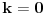
.
2)
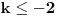
Malo ću izmeniti oznake radi lakšeg snalaženja. Dokazaću sledeće:
Ne postoji funkcija
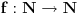
za koju važi:
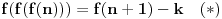
gde je
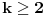
unapred zadati prirodan broj.
Dokaz:
Najpre indukcijom po

dokazujemo sledeće tvrđenje:
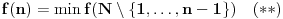
Pretpostavimo da postoji broj
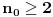
takav da je
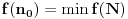
. Uvrštavajući
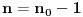
u relaciju
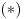
imamo:
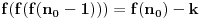
pa dobijamo kontradikciju. Dakle, tvrđenje zaista važi za

. Pretpostavimo da važi za sve brojeve manje od

i dokazujemo istinitost za

. Opet pretpostavimo da postoji
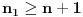
za koje važi
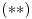
. Uvrštavajući
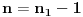
u
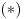
imamo:
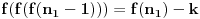
Primetimo da ako
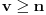
onda mora biti i
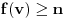
, jer je

(na osnovu indukcijskih hipoteza). Kako je
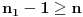
, to je i
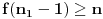
, pa je i
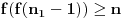
. Time smo dobili kontradikciju, pa je dokaz tvrđenja
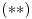
završen. Primetimo da štaviše važi stroga nejednakost, i da ovo tvrđenje neposredno implicira da je

rastuća.
Neka je niz
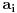
dat rekurentnom formulom
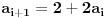
,
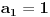
. Dokazaćemo indukcijom po

da za sve

i sve
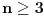
važi sledeće tvrđenje (koje neposredno implicira da takva funkcija ne postoji):
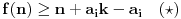
Uvrštavajući

u jednakost
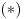
imamo
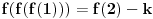
, pa mora biti
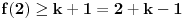
, a pošto je funkcija rastuća za sve
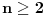
važi
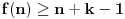
. Pretpostavimo da
važi za

. Za bilo koje
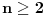
iz
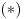
imamo:
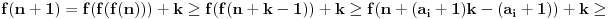
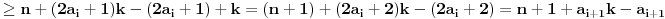
3) Parno
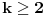
Evo ga ono baksuzno :)
Neka je
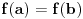
. Tada je i
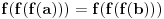
, odnosno
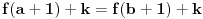
iz čega dobijamo i
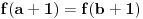
, pa iteracijom zaključujemo da važi i
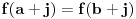
za sve
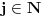
. Imamo dve mogućnosti: ili je

periodična (počevši od neke tačke) ako je
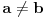
ili je injektivna.
Pretpostavimo da je periodična. Tada uzima konačan skup vrednosti. Neka je
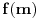
najveća od njih. Ukoliko je
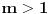
uvrštavanjem
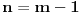
u datu funkcionalnu jednačinu dobijamo da je
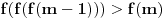
, kontradikcija. Dakle,
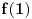
je jedina najveća slika. Neka je
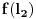
druga po veličini (ne mora biti jedinstvena). Iz polazne jednačine dobijamo
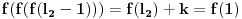
(u suprotnom
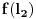
ne bi bila druga po veličini), pa pošto je
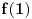
jedinstvena sledi da postoji broj (konkretno
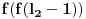
je u pitanju) koji se slika u

. Takođe primetimo da se prva dva po veličini elementa razlikuju baš za

, a slično, ako je
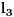
treći po veličini onda važi
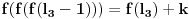
pa je i razlika drugog i trećeg po veličini upravo

, i tako sve do kraja. Dakle, skup vrednosti posmatrane funkcije je skup
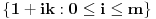
, gde je

neki prirodan broj, i pri tome je
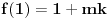
. Neka je

period funkcije.
Pretpostavimo da se samo
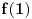
nalazi van periodičnog dela. Tada je
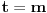
. Dalje, imamo da važi:
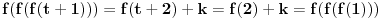
S druge strane, takođe važi
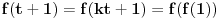
. Iz ovog i prethodnog sledi da je
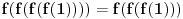
, odnosno
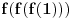
je fiksna tačka ove funkcije. Pokušajmo da nađemo prvu iteraciju
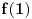
koja je fiksna tačka. Primetimo da je nemoguće
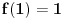
, kao i
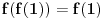
(ovo drugo sledi iz jedinstvenosti
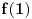
), pa nam preostaje
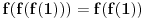
ili
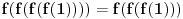
. U oba slučaja dolazimo do situacije da je
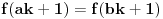
za neke različite
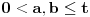
. To dalje znači
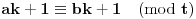
, odnosno
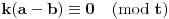
. Kako je
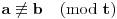
, preostaje nam jedino da je
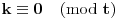
. Međutim, to znači

. Dakle, svi ovi brojevi se preslikavaju u istu sliku, recimo

. Ne može biti
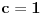
jer bi tada bilo
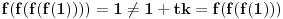
. Važi
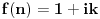
za sve
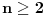
. Ako je
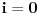
onda imamo
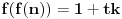
, odnosno
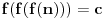
, dok za

odmah važi
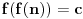
, pa i
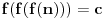
. Međutim, to dalje znači da za proizvoljne različite
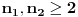
imamo
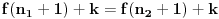
, pa i
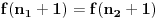
. Kontradikcija.
Dakle, bar još
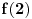
se ne ubraja u periodičnost, odnosno vrednost
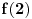
je jedinstvena. Neka je
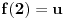
. Ako je
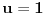
onda iz jedinstvenosti
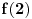
i činjenice da je
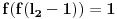
imamo da je
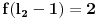
. Za
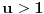
uzmimo

takvo da je
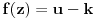
. Stavljajući
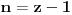
u početnu funkcionalnu jednačinu, dobijamo da je
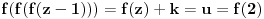
, pa opet iz jedinstvenosti
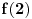
imamo da je
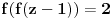
. U oba slučaja smo dobili kontradikciju, jer, kako je ranije pokazano, broj

ne pripada skupu vrednosti posmatrane funkcije.
Time je dokazano da je

injekcija.
Neka je, dalje,
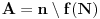
,
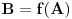
, i
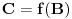
. Ovi skupovi su međusobno disjunktni, a pošto je

injekcija, važi
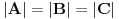
. Očigledno je
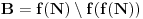
i
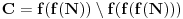
. Pošto je
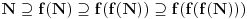
, imamo da je
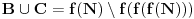
. Primetimo još i da iz date funkcionalne jednačine sledi
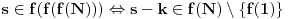
.
Za
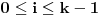
definišimo
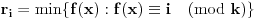
. Označimo još i
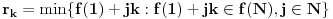
. Može se dogoditi i da neko
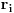
ne postoji, i u tom slučaju ga jednostavno nadalje ignorišemo. Tvrdimo da je
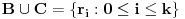
. Za početak, očigledno je da
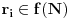
za sve
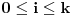
. S druge strane, ako bi za neko

važilo
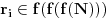
, onda bismo imali
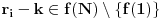
, što je u kontradikciji sa minimalnošću
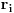
. Proverimo sada da li neki element različit od svih
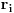
pripada posmatranoj uniji. Predstavimo ga u obliku
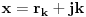
ukoliko je to moguće, odnosno ako to nije moguće u obliku
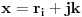
za neko
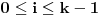
, gde
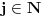
. Tada važi
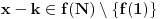
, pa sledi
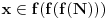
, odnosno
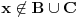
.
Dakle,

ima konačno mnogo elemenata, pa to važi i za

, odnosno svi sem konačno mnogo prirodnih brojeva su sadržani u skupu slika funkcije

. Zaključujemo da svi
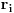
postoje, pa

ima baš
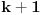
elemenata. Međutim, kako su

i

disjunktni i sa istim brojem elemenata, njihova unija mora sadržati paran broj elemenata, dok je
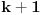
neparno. Kontradikcija!
Moj duboki naklon i beskonačno divljenje svima koji su uspeli da ovo pročitaju do kraja :) Ako neko uspe da nađe jednostavnije rešenje od ovog ili bar da uprosti neki korak rešenju neka se ne ustručava da to ovde napiše, ja eto nisam uspeo. Naravno, kao i uvek ću rado otkloniti bilo kakve eventualne nejasnoće u vezi sa ovim mojim rešenjem.
Ljubičice crvena, što si plava kô zelena trava.
 postoji funkcija
postoji funkcija 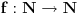 takva da važi
takva da važi 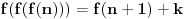 .
.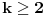 , ostale sam rešio (neću još da napišem rešenje da bi svako sam mogao da pokuša, ako ne uspete a zanima vas javite). Nagađam da za njih nema rešenja, ali nikako mi ne uspeva da dokažem. Najdalje što sam stigao u tom slučaju je da funkcija mora biti injektivna (ovo možete slobodno koristiti ako vam zatreba u rešavanju pošto za to imam dokaz). Takođe, dovoljno je pokazati da je
, ostale sam rešio (neću još da napišem rešenje da bi svako sam mogao da pokuša, ako ne uspete a zanima vas javite). Nagađam da za njih nema rešenja, ali nikako mi ne uspeva da dokažem. Najdalje što sam stigao u tom slučaju je da funkcija mora biti injektivna (ovo možete slobodno koristiti ako vam zatreba u rešavanju pošto za to imam dokaz). Takođe, dovoljno je pokazati da je 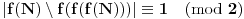 , ali ni to nisam uspeo. Ako se zaglavite na istom mestu kao i ja pokušajte da rešite bar ove slučajeve koje sam i ja rešio, da uporedimo razmišljanja, i, naravno, kao i uvek dobrodošao je i svaki, makar i neuspešan pokušaj, a ne isključivo gotova rešenja :)
, ali ni to nisam uspeo. Ako se zaglavite na istom mestu kao i ja pokušajte da rešite bar ove slučajeve koje sam i ja rešio, da uporedimo razmišljanja, i, naravno, kao i uvek dobrodošao je i svaki, makar i neuspešan pokušaj, a ne isključivo gotova rešenja :)



 Za koje k funkcionalna jednačina ima rešenja?
Za koje k funkcionalna jednačina ima rešenja?