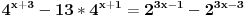@nigga10,
ako mogu dobro da primetim, ovde imas u drugoj jednacini clanove s leve strane koji su u prvoj kvadrirani. valjda je to da zbuni protivnika

logicno je da druga bude iznad prve.
znaci mozes da uvedes zamenu:
druga jednacina je
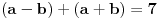
a prva
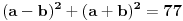
iz ovoga lagano dobijes a i b, dobijes koje su vrednosti prvog i drugog clana, logaritmujes, i dobijes x i y. valjda je to to.