Citat:
Nedeljko:
Razmatranje nekih matematičkih pitanja u svetlu aksiomatske teorije skupova bez aksiome izbora ili uz ostale aksiome teorije skupova + neka zamena za aksiomu izbora (nekim slabijim ili jačim oblikom) imaju smisla, kao i diskutovanje nekih drugih jakih aksioma teorije skupova. Međutim, to može imati smisla samo u aksiomatskoj teoriji skupova kada se tačno zna koje se aksiome koriste.
Citat:
uranium:
Detaljnom analizom upotrebljenih argumenata se (verovatno) može ustanoviti da li bi isti zasključak važio i u bilo kojoj poznatoj aksiomatskoj teoriji skupova ili ne.
Sa ovim se, naravno, slažem. Ono što sam pisao u prošloj poruci nije se odnosilo na izučavanje nekog problema sa formalnog stanovišta, već na rešavanje problema bez spuštanja na tako niske nivoe. Da navedem i primer koji mi je trenutno pao na pamet. Pitanje je da li Košijeva funkcionalna jednačina ima rešenje različito od identičke funkcije. Odgovor, kakav sam video na većini mesta, je: "Da, ukoliko prihvatimo aksiomu izbora". Ja bih na postavljeno pitanje odgovorio sa da, bez suvišnih komentara, jer aksioma izbora jeste prihvaćena. To i dalje ne sprečava (a i ne bi trebalo da sprečava) formaliste da gledaju šta bi bilo kad bi bilo, ali smatram da je prilikom ovakvog pitanja postavljenog u ovakvom kontekstu drugi deo odgovora savršeno bespotreban.
Citat:
Nedeljko:
Dopusti da razni ljudi imaju razna mišljenja.
Pre nekog vremena pričali smo o hipotezi kontinuuma, koja se meni lično sviđa i smatram da bi trebala da bude prihvaćena. Vudinu se, primera radi, ne sviđa i smatra da bi njena negacija trebala da bude prihvaćena (ovo "sviđa" i "ne sviđa" govorim više metaforično, bez zalaženja u razloge za i protiv). Zamislimo da se jednoga dana postigne konsenzus da bude po njegovom. E, od tog momenta ću ja, prilikom rešavanja zadataka, koristiti negaciju hipoteze kontinuuma, bez obzira na to što se moje mišljenje razlikuje od opšteprihvaćenog. Zaključak, svakako da ne branim da razni ljudi imaju razna mišljenja, ali mislim da formalistima treba prepustiti da se igraju aksiomama dok ostale ne treba da je briga za to već samo treba da slede prihvaćene principe iako eventualno mogu da se ne slažu sa njima.
Citat:
uranium: offtopic:
Nisam nikad čuo za teoriju skupova bez npr. aksiome unije.
Evo, možeš i sam da napraviš jednu. Recimo, uzmi neku već postojeću i izbaci aksiomu unije, nazovimo ovo npr. Uraniumova aksiomatika. Sad mene zanima zašto bi, recimo, ZF bez C bila bitnija od Uraniumove aksiomatike. Pretpostavljam da ćeš reći da je to zbog toga što ova prva ima nekog smisla a druga nema, ali tu sledi deo gde se verovatno ne slažemo. Ja kažem da za formaliste (koliko li sam puta upotrebio ovu reč) sve ima podjednakog smisla dok za ostatak matematičkog sveta jedna i samo jedna teorija ima smisla dok ostale nemaju, ili bi bar tako trebalo da bude.
Ljubičice crvena, što si plava kô zelena trava.
Re: Skup R je neprebrojiv!
) da skup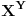 
bude neprazan.
Registrovani: 3 ( Nebojsa Milanovic, bojanum, bakara )
