Citat:
djoka_l: Druže majore,
pohvalno j e što si odlučio da malo istražiš teoriju pre nego što se ponovo baciš na komprimovanje slučajnog niza (kao što si pre pokušavao).
Druze djoka_I, nemam pojma o cemu pricas:
http://sr.wikipedia.org/w/inde...&action=edit&redlink=1
Deluje mi da si malo odlutao od zadatka za sta sam verovatno ja kriv zbog nevestog nacina postavljanja, pa da ponovim preciznije: kad odredim nivo entropije nekog signala, a uzimajuci u obzir matematicku teoriju informacija, na koji nacin, kako, uz pomoc koje jednacine mi nivo entropije oblikuje teoretski minimum sa kojim ta ista informacija moze da se opise.?
Citat:
Međutim, potrebno je da još malo proučiš materiju, pre nego što tvoj algoritam proradi.
Radi savrseno, hvala na propitivanju, tj, program uradjen po algoritmu radi savrseno, doduse ne po onom koji sam predstavio na es-u. Ako se dobro secam, a secam se, tvoja primedba u jednoj od rasprava koju sam pokrenuo je bila da je glavni problem sa algoritmom da on ni ne postoji, pa ako ne postoji ne moze ni da proradi?
Citat:
Vidim da ne razumeš pojam simbola, pa da ti malo razjasnim.
Nauci me kaludjeru moj
http://www.youtube.com/watch?v=EuyEapqJOcE
Citat:
Kada imaš binarni signal i posmatraš poruku bit po bit (u tvom slučaju gledaš samo simbole t i z, a to možemo i da interpretiramo kao 0 1)
a mozemo da interpretiramo i kao z u, u i, i o, o p, tj. bilo koja dva simbola, tacno netacno, ima napon nema napon, itd... ja bih rekao simbol po simbol, a ne bit po bit? (mozemo da interpretiramo kao 0 1 ali zasto bi, ako je jedina operacija kodovanje tj. zamena jednog niza drugim, zasto bi smo uvodili binarni brojni sistem ako necemo operisati nad brojevima i koristiti racunske operacije? t i z su sasvim lepa slova kao sto su i 0 i 1 lepi brojevi.)
Citat:
nikakvu kompresiju ne možemo da ostvarimo jer jedan bit informacije ne možemo da predstavimo sa manje od jednog bita.
Ali ja to nisam ni tvrdio?
Citat:
Kolikva god da je frekvencija pojavljivanja jednog ili drugog simbola, ne možeš uzeti da je jedan signal, na primer t predstavljen sa 0.2 bita, a drugi sa 8 bita,
Ko kaze da ne mogu, to je stvar konvencije?
Citat:
pa da ostvariš kompresiju drugačijim kodiranjem,
Naravno, kompresija se moze ostvariti samo i iskljucivo drugacijim kodiranjem?
Citat:
nego mora biti po jedan bit.
"Biti po jedan bit"? Eh te jezicke zavrzlame.
Citat:
Sa druge strane, kada se kaže "signal" u teoriji informacija se ne podrazuma jedan bit informacije nego jedan simbol iz skupa simbola.
Ne bih rekao. Kad se kaze "signal" u teoriji informacija a i inace, misli se na signal iliti poruku tj, niz simbola a ne na jedan simbol iz skupa simbola. ispravi me ako gresim? "Signal" je signal, a simbol je simbol, "signal" nije jedan simbol iz skupa simbola kao sto si ti napisao.
Citat:
Zamisli situaciju da meteorološka stanica treba da pošalje jedan podatak koji predstavlja vreme, i da to vreme uzima jednu od vrednosti iz skupa, sunčano, oblačno, kiša, sneg.
Ti za pocetak zamisli situaciju da ljudi resavaju zadatke koji su postavljeni, a ne neke druge.
Citat:
Dakle, imamo skup od 4 "simbola" i treba da ih kodiramo na neki način.
Ne, nego imamo skup od 4 vrednosti, i mozda hocemo da ih kodiramo na neki nacin, prilagodjeno kanalu prenosa ili primaocu poruke.
Citat:
Pošto imamo 4 različita ishoda eksperimenta, tada su nam potrebna dva bita, pa recimo da te ishode kodiramo kao 00, 01, 10 i 11.
Mislim da ti nedostaje par reci: "najmanje", "sa istim verovatnocama pojavljivana" i "binarni brojni sistem". Kao na primer: posto "imamo" 4 razlicita ishoda eksperimenta, sa istim verovatnocama pojavljivanja, tada su nam potrebna
najmanje dva bita (simbola?) za kodovanje tih vrednosti, tj. ishoda eksperimenta, pa recimo da te ishode kodiramo kao: tt, tz, zt, zz ili tt, tzt, ztzz i zztzztzztzz, ili 0, 1, 2, 3 ili a, b, c, d ili itd...
Citat:
E sada, ako ta meteorološka stanica radi u pustinji, ona će najčešće slati poruku 00, ponekad 01, vrlo retko 10, a skoro nikada 11. Dakle, ima smisla da se sunčano vreme kodira sa jednim bitom, na primer 0, a da se ova druga tri vremena kodiraju sa više od dva bita, pa bi se pri tome poruka "komprimovala".
Pa, sad, sve zavisi, moram prvo da dohakam da si ti zamislio da meteoroloska stanica svakodnevno ili vise puta u toku dana meri vreme i salje informaciju o istom. U suprotnom ako bi m. stanica merila vreme 6 puta godisnje ili na primer sve ukupno 6 puta, s tim sto bi tih 6 puta bilo rasporedjeno bas pocetkom kisne sezone koja opet traje 2 nedelje godisnje, dosli bi do ovoga: 3 puta suncano, 2 puta oblacno, 1 puta kisa, 0 puta sneg. Ima smisla da se suncano vreme kodira sa jednim bitom (simbolom) ako bi izvestaj o tome isao 345 puta u godini, ali ako bi isao tri puta godisnje? Na matematickom smo forumu, izvoli izracunaj, ako suncano vreme kodiras sa 1 simbolom, a ova druga tri vremena sa vise od dva simbola, koliko godina vremena treba da prodje da bi mogao da racunas da ti je poruka "komprimovana" kao sto si lepo napisao?
Citat:
Dakle, posmatraj malo, umesto bit po bit, poruku kao grupu bitova, pa ćeš videti da se pojavljuju drugačije vrednosti entropije.
Da pokusam: posmatracu poruku: 1.)ttttttttttttttttttttttttzzzzzzzzzzzzzzzzzzzzzzzz za koju sam utvrdio da je entropija jednako 1:
a) grupa "bitova" (simbola) duzine dva: tt 12 puta, tz nula puta, zt nula puta (pa tz i zt ne ucestvuju u racunici) i zz 12 puta, sve ukupno 24 grupe od po dva simbola. Racunam entropiju:
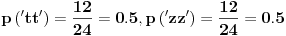
pa je
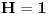
[bita/simbol]
b) grupa "bitova" (simbola) duzine tri: ttt: osam puta, ttz, tzt, tzz, ztt, ztz, zzt nula puta, zzz osam puta. Sve ukupno: 16 grupa od po tri simbola.
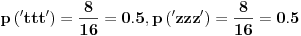
pa je
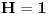
[bita/simbol]
c) grupa "bitova" (simbola) duzine cetri: ... itd...
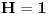
I dalje je entropija 1 pa bi signal ( poruka ) trebao biti nekompresabilan, ali je u realnosti veoma kompresabilan kao sto smo videli na vecem primeru.
Citat:
Recimo tvoja poruka od 24 slova t i 24 slova z u prvom slučaju ima verovatnoću pojavljivanja 24 slova t u nizu 1/2 i 24 slova z u nizu 1/2, pa je moguće da (pošto ima samo dva moguća ishoda) se svaki od mogućih ishoda kodira samo sa jednim bitom.
"poruka od 24 slova t i 24 slova z u prvom slučaju" rekao bih da nema verovatnocu pojavljivanja 24 slova t u nizu 1/2, vec izvesnost da se pojavilo 24 simbola t i 24 simbola z, a nikakvu verovatnocu bilo kakvog pojavljivanja. poruka je zavrsena i ne planira se bilo kakvo novo emitovanje simbola t ili z.
Citat:
pa je moguće da (pošto ima samo dva moguća ishoda)
samo dva moguca ishoda
cega???
Citat:
se svaki od mogućih ishoda kodira samo sa jednim bitom.
Iskreno receno mislim da i celu poruku mozes da kodiras samo sa jednim bitom, ako se bavis kodiranjem, ali i kodiranje kao operacija ima svoja pravila i uslove...
Jos jednom za one sa rasutom paznjom zadatak je: Na osnovu nivoa entropije nekog signala, a uzimajuci u obzir matematicku teoriju informacija, na koji nacin, kako, uz pomoc koje jednacine mi nivo entropije oblikuje teoretski minimum sa kojim ta ista informacija moze da se opise?
Nemoj da pricas?