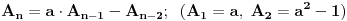[es] - determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

Mali Misha
Mihajlo Anđelković
NBGD

Član broj: 79396
Poruke: 379
89.190.198.*

ICQ: 195487525
Sajt: cpptea.com

+1 Profil

determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{11.12.2006. u 21:42 - pre 211 meseci}

Dakle data je determinanta:

Pri čemu je determinanta dimenzije n x n. Zadatak je izračunati je. Jedno rekurzivno rešenje se lako nalazi razvojem po prvoj koloni:

Ali, da li je to sve što se u ovom zadatku očekuje? Kako ga naći, ukoliko postoji ne-rekurzivno rešenje?

Ipak se ++uje.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.ADSL.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+605 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{12.12.2006. u 10:31 - pre 211 meseci}

Ti si samo postavio rekurentnu formulu. Očekuje se i da je rešiš.

Rešavanjem ovog sistema dobijaš:

Prema tome, rešenje determinante je:

Ako ti je ovo za domaći pa profesor neće da prihvati rešavanje rekurentne jednačine (recimo, ako to još niste učili), ti se „napravi lud“ pa počni od ovog rešenja što sam ti dao i dokaži ga indukcijom.

_{[Ovu poruku je menjao Bojan Basic dana 12.12.2006. u 12:38 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*

+6 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{12.12.2006. u 10:47 - pre 211 meseci}

Bojane, možda ne bi bila zgoreg i mala diskusija o rešivosti? Tvoje rešenje važi samo ako

, ali šta se dešava za

i za

? (Zadatak ničim ne ograničava domen za

.)

Dodatak: Tj. nominalno formula važi i za

, ali se može uprostiti.

Odgovor na temu

Mali Misha
Mihajlo Anđelković
NBGD

Član broj: 79396
Poruke: 379
89.190.198.*

ICQ: 195487525
Sajt: cpptea.com

+1 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{12.12.2006. u 10:48 - pre 211 meseci}

Stvarno hvala na iscrpnim objašnjenjima. : )
To danas čini nedostatak literature..

Ipak se ++uje.

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*

+6 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{12.12.2006. u 11:58 - pre 211 meseci}

Ne znam da li je Bojan prevideo moju prethodnu poruku?

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.ADSL.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+605 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{12.12.2006. u 12:01 - pre 211 meseci}

nema nikakvih problema. Za

ću rešiti sad.

Rešavanjem ovog sistema se dobija (naravno, vodeći računa da je

Prema tome, rešenje determinante je:

Međutim, možda nije zgoreg napomenuti da je suvišno čak i ovo izdvajati kao poseban slučaj, jer je lako proveriti da je

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*

+6 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{12.12.2006. u 12:16 - pre 211 meseci}

Stoji ovo poslednje što si rekao, ali je poenta više bila u tehnici rešavanja rekurzivnih jednačina, gde se po pravilu slučaj višestrukih korena zasebno obrađuje

Odgovor na temu

uranium
Beograd

Član broj: 60097
Poruke: 543
*.eunet.yu.

Jabber: uranium@elitesecurity.org
ICQ: 324386953

+5 Profil

Re: determinanta n-tog reda: postoji li ne-rekurzivno rešenje?

^{14.12.2006. u 06:02 - pre 211 meseci}

Skoro sam nešto kopao po knjizi The theory of determinants in the historical order of development - Thomas Muir i naišao na jedno uopštenje ovog zadatka:

To uopštenje se pojavilo u radu iz 1878. - Scott R. F., On some symmetrical forms of determinants, Messenger of Math, viii. pp. 131-138., rešenje tog dela je naravno primena identične tehnike koju je već opisao Bojan Basic a u momentu kad se pojavilo nije izazvalo pohvale, jer je rezultat izgleda većim delom već bio poznat.

Takođe, u knjizi A book of mathematical problems - Wolstenholme J. iz 1867. kao jedan od zadataka pojavljuje se izračunavanje determinante:

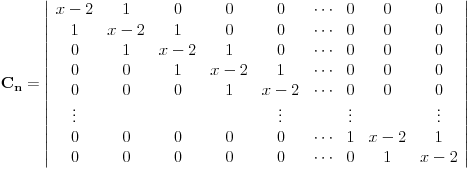
Na kraju, da pomenem da postoji direktna veza između polazne determinante

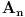
i Čebiševljevih polinoma druge vrste a to nam daje još nekoliko formula za izračunavanje

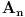
- za detalje pogledati Chebyshev Polynomial of the Second Kind

_{[Ovu poruku je menjao uranium dana 14.12.2006. u 07:14 GMT+1]}

_{Attempt all the problems. Those you can do, don't do. Do the ones you cannot.}

Odgovor na temu