Odosmo u offtopic.
Nekoliko istorijskih činjenica:
•
Jacob Bernoulli u jednom od pisama
Leibniz-u postavlja pitanje: Kakav bi bio smisao
Leibniz-ove teoreme o

-tom izvodu proizvoda dve f-je, ako

ne bi bilo celo?
•
Leibniz u pismima
L'Hôpital-u (iz 1695. god.) i
Wallis-u (iz 1697. god.) primećuje da je moguće definisati izvod reda
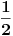
.
• Prvi uspeh postiže
Euler (1738. god.) zapažanjem da
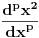
ima smisla i kad

nije celo.
• Neke zanimljive predloge dao je i
Laplace (1812. god.).
•
Lacroix je izveo eksplicitnu formulu za
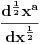
(1820. god.).
•
Liouville (1822. god.) iznosi svoj prvi predlog definicije uopštenog izvoda, a u periodu od 1832. do 1837. objavljuje niz radova na tu temu - koji se zasnivaju na osnovnoj ideji: ako f-ju predstavimo u obliku
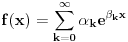
, onda je (uz izvesne pretpostavke o konvergenciji) uopšteni izvod jednak
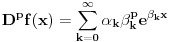
(
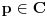
).
Zaista nemam živaca da pišem ovo dalje - koga ova oblast stvarno zanima (a pri kraju je sa postdipl. iz
Analize 
) preporučio bih knjigu
Integraly i proizvodnye drobnogo poryadka,
S. G. Samko, A. A. Kilbas, O. I. Marichev.
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.