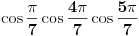 ili
ili 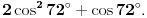
Neka je
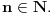 Jednačina
Jednačina 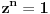 u polju kompleksnih brojeva ima
u polju kompleksnih brojeva ima  rešenja koja se izražavaju sa
rešenja koja se izražavaju sa 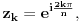 gde
gde 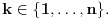 Rešenja te jednačine se zovu
Rešenja te jednačine se zovu  -ti koreni iz jedinice. One od njih koji nisu
-ti koreni iz jedinice. One od njih koji nisu  -ti koreni ni za jedno
-ti koreni ni za jedno 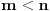 zovemo i primitivnim
zovemo i primitivnim  -tim korenima iz jedinice. To su tačno brojevi oblika
-tim korenima iz jedinice. To su tačno brojevi oblika 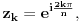 gde je
gde je  uzajamno prosto sa
uzajamno prosto sa 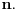 Polinom
Polinom 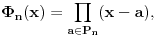 gde je
gde je 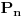 skup primitivnih
skup primitivnih  -tih korena iz jedinice zovemo polinomom deobe kruga na
-tih korena iz jedinice zovemo polinomom deobe kruga na  jednakih delova.
jednakih delova.Nije teško pokazati da za svaki prirodan broj
 važi
važi 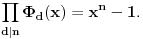 Odatle dobijamo rekurentnu formulu za računanje polinoma deobe kruga.
Odatle dobijamo rekurentnu formulu za računanje polinoma deobe kruga.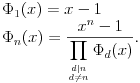
Pomoću ove formule indukcijom se dokazuje da svi polinomi deobe kruga imaju celobrojne koeficijente među kojima je vodeći jednak jedinici.
Dakle,
 je jedan algebarski identitet sa racionalnim koeficijentima. Pritom ne postoji niti jedan algebarski identitet za
je jedan algebarski identitet sa racionalnim koeficijentima. Pritom ne postoji niti jedan algebarski identitet za 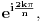 gde je
gde je  uzajamno prosto sa
uzajamno prosto sa 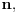 sa racionalnim koeficijentima nižeg stepena osim identiteta
sa racionalnim koeficijentima nižeg stepena osim identiteta 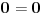 . Recimo, ako je
. Recimo, ako je 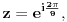 budući da je
budući da je 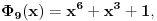 možemo biti sigurni da je na primer
možemo biti sigurni da je na primer 
Međutim, minimalnost stepena tu nije lako dokazati. Ta činjenica je ekvivalentna sa činjenicom da se polinom deobe kruga ne može zapisati kao proizvod dva polinoma sa racionalnim koeficijentima stepena najmanje jedan. Da bi se to dokazalo, neophodno je dokazati najpre sledeće pomoćno tvrđenje:
Gausova lema: Neka je
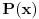 polinom sa celim koeficijentima. Tada se on može prikazati kao proizvod dva polinoma stepena bar jedan sa racionalnim koeficijentima ako i samo ako se može prikazati kao proizvod dva polinoma stepena bar jedan sa celim koeficijentima.
polinom sa celim koeficijentima. Tada se on može prikazati kao proizvod dva polinoma stepena bar jedan sa racionalnim koeficijentima ako i samo ako se može prikazati kao proizvod dva polinoma stepena bar jedan sa celim koeficijentima.Dokaz: Nekonstantan celobrojan polinom zvaćemo primitivnim ako ne postoji prost broj koji deli sve njegove koeficijente. Najpre pokažimo da je proizvod dva primitivna polinoma primitivan polinom.
Neka su
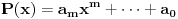 i
i 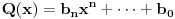 primitivni polinomi i
primitivni polinomi i  njihov proizvod. Ako je
njihov proizvod. Ako je  prost broj, onda po pretpostavci postoje najmanji indeksi
prost broj, onda po pretpostavci postoje najmanji indeksi 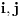 takvi da
takvi da 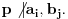 No, tada će
No, tada će 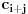 biti zbir nekih sabiraka deljivih sa
biti zbir nekih sabiraka deljivih sa  i broja
i broja 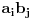 koji nije deljiv sa
koji nije deljiv sa 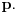
Neka je sada
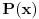 celobrojan polinom i pritom neka je
celobrojan polinom i pritom neka je 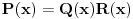 za neke polinome sa racionalnim koeficijentima stepena barem jedan. Pretpostavimo da su njihovi nenula koeficijenti zapisani u vidu količnika uzajamno prostih celih brojeva. NZD brojilaca koeficijenata iz polinoma
za neke polinome sa racionalnim koeficijentima stepena barem jedan. Pretpostavimo da su njihovi nenula koeficijenti zapisani u vidu količnika uzajamno prostih celih brojeva. NZD brojilaca koeficijenata iz polinoma 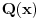 označimo sa
označimo sa  , NZS imenilaca sa
, NZS imenilaca sa  , brojilaca koeficijenata polinoma
, brojilaca koeficijenata polinoma 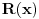 sa
sa 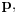 a NZS imenilaca sa
a NZS imenilaca sa 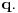 Tada će brojevi
Tada će brojevi 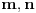 biti uzajamno prosti, kao i
biti uzajamno prosti, kao i 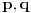 , a polinomi
, a polinomi  i
i 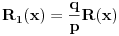 će biti celobrojni i primitivni. No, tada će i polinom
će biti celobrojni i primitivni. No, tada će i polinom 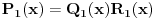 biti primitivan, a otuda i pošto je
biti primitivan, a otuda i pošto je 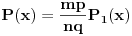 celobrojan polinom, razlomak
celobrojan polinom, razlomak 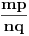 mora biti ceo broj. No, tada je polinom
mora biti ceo broj. No, tada je polinom 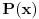 proizvod celobrojnih polinoma
proizvod celobrojnih polinoma 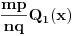 i
i 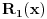 stepena barem jedan.
stepena barem jedan.Od mene zasad ovoliko, nastaviću drugi put.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Polinom deobe kruga i Gausova lema
Polinom deobe kruga i Gausova lema