U ovom gore primeru NE MOŽEMO reći da
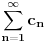
divergira, već samo ne znamo da li konvergira, tj. ne zadovoljava Lajbnicov kriterijum konvergencije, ali to ne znači da divergira, već se moraju koristiti neki drugi kriterijumi ili se koristiti kriterijum poređenja sa redovima koji su manji/veći od ovog.
Bar tako mislim da jeste, davno je bilo kad sam ovo učio na faksu.
Potom, drugi korak nije dobar, jer čemu je jednako
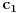
, već bi trebalo da stoji:
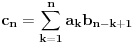
međutim, to ne menja mnogo rezultat.
Ako se napravi tabela koja u prvoj koloni (osim prvog elementa prve vrste) sadrži članove reda
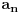
, a u prvoj vrsti (osim elementa prve kolone) sadrži članove reda
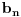
, dok se u ostalim poljima tabele nalaze proizvodi elemenata početnog niza koji se nalaze u na početku te vrste i kolone, tada elementi reda
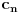
predstavljaju redom (koordinate u tabeli su date ne računajući prvu vrstu i kolonu):
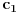
- element na poziciji 1-1
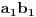
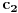
- suma elemenata 1-2 i 2-1
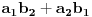
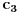
- suma elemenata 1-3, 2-2 i 3-1
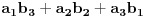
Dakle, k-ti element novog reda je suma elemenata na liniji paralelnoj sporednoj dijagonali koja sadrži elemente
.
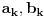
Međutim, šta ako kažemo da je
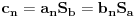
(svaki član novog reda je suma elemenata po vrsti ili po koloni tabele), tada se može primeniti Lajbnicov kriterijum i novi red konvergira.
Dakle, kako god menjali redosled sumiranja, ne možemo dokazati da proizvod dva polazna reda divergira, nego samo možemo namestiti opšti član tako da za njega ne važi Lajbnicov kriterijum, ali to nije dokaz da taj red divergira.
Možda sam negde pogrešio u ovom zaključivanju, pa ako neko primeti, neka me ispravi.
Blessed are those who can laugh at themselves, for they shall never cease to be amused.
Proizvod konvergentnih redova
Registrovani: 2 ( Java Beograd, djoka_l )
